题目内容
10.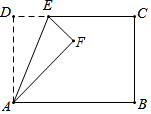 如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为$\frac{5}{2}$或10.
如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为$\frac{5}{2}$或10.
分析 分两种情况讨论:点F在矩形内部;点F在矩形外部,分别根据折叠的性质以及勾股定理,列方程进行计算求解,即可得到DE的长.
解答  解:分两种情况:
解:分两种情况:
①如图1,当点F在矩形内部时,
∵点F在AB的垂直平分线MN上,
∴AN=4;
∵AF=AD=5,
由勾股定理得FN=3,
∴FM=2,
设DE为y,则EM=4-y,FE=y,
在△EMF中,由勾股定理得:y2=(4-y)2+22,
∴y=$\frac{5}{2}$,
即DE的长为$\frac{5}{2}$.
②如图2,当点F在矩形外部时,
同①的方法可得FN=3,
∴FM=8,
设DE为z,则EM=z-4,FE=z,
在△EMF中,由勾股定理得:z2=(z-4)2+82,
∴z=10,
即DE的长为10.
综上所述,点F刚好落在线段AB的垂直平分线上时,DE的长为$\frac{5}{2}$或10
故答案为:$\frac{5}{2}$或10.
点评 本题以折叠问题为背景,主要考查矩形的性质、翻折变换的性质、勾股定理等几何知识的综合应用;解决问题的关键利用直角三角形,运用勾股定理列方程求解.

练习册系列答案
相关题目
15.一次函数y=kx+b与反比例函数$y=\frac{m}{n}$中,若x与y的部分对应值如下表:
则不等式$\frac{m}{x}>kx+b$的解集是x<-4或0<x<1.
| x | … | -4 | -2 | -1 | 1 | 2 | 4 | … |
| y=kx+b | … | -1 | 1 | 2 | 4 | 5 | 7 | … |
| $y=\frac{m}{x}$ | … | -1 | -2 | -4 | 4 | 2 | 1 | … |
2.从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
根据以上数据可以估计,该玉米种子发芽的概率约为0.80(精确到0.10).
| 种子粒数 | 100 | 400 | 800 | 1000 | 2000 | 5000 |
| 发芽种子粒数 | 85 | 318 | 652 | 793 | 1604 | 4005 |
| 发芽频率 | 0.850 | 0.795 | 0.815 | 0.793 | 0.802 | 0.801 |
20.下列图形中不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 实数a在数轴上的位置如图,化简$\sqrt{(a-2)^{2}}$+a=2.
实数a在数轴上的位置如图,化简$\sqrt{(a-2)^{2}}$+a=2. 如图,在Rt△ABC中,AB=AC=4,∠BAC=90°,点E为AB的中点,以AE为对角线作正方形ADEF,连接CF并延长交BD于点G,则线段CG的长等于$\frac{8\sqrt{10}}{5}$.
如图,在Rt△ABC中,AB=AC=4,∠BAC=90°,点E为AB的中点,以AE为对角线作正方形ADEF,连接CF并延长交BD于点G,则线段CG的长等于$\frac{8\sqrt{10}}{5}$.