Question

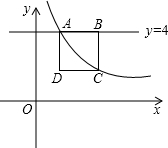如图，直线y=4和反比例函数y=

8

x

的图象交于点A，点B为直线y=4上的一点，点B在点A的右边，AB=m．
（1）求点B的坐标（用含m的代数式表示）；
（2）以AB为边向下做正方形ABCD，若点C落在反比例函数y=

8

x

的图象上，求m的值和点C的坐标．

Answer 1

考点：反比例函数与一次函数的交点问题

专题：

分析：（1）由直线y=4和反比例函数y=

8

x

的图象交于点A，可求得点A的坐标，继而可求得点B的坐标；
（2）由以AB为边向下做正方形ABCD，可求得点C的坐标，又由点C落在反比例函数y=

8

x

的图象上，即可得方程：4-m=

8

2+m

，解此方程即可求得答案．

解答：解：（1）∵直线y=4和反比例函数y=

8

x

的图象交于点A，
∴4=

8

x

，
解得：x=2，
∴点A（2，4），
∵点B在点A的右边，AB=m，
∴点B的坐标为：（2+m，4）；

（2）∵四边形ABCD是正方形，
∴BC=AB=m，
∴点C的坐标为：（2+m，4-m），
∵点C落在反比例函数y=

8

x

的图象上，
∴4-m=

8

2+m

，
解得：m₁=2，m₂=0（舍去），
∴m=2，点C的坐标为（4，2）．

点评：此题考查了反比例函数与一次函数的交点问题以及待定系数法求函数的解析式．此题难度适中，注意掌握数形结合思想与方程思想的应用．