题目内容
18.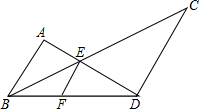 如图,F在BD上,BC、AD相交于点E,且AB∥CD∥EF,
如图,F在BD上,BC、AD相交于点E,且AB∥CD∥EF,(1)图中有哪几对位似三角形,选其中一对加以证明;
(2)若AB=2,CD=3,求EF的长.
分析 (1)利用相似三角形的判定方法以及位似图形的性质进而得出答案;
(2)利用比例的性质以及相似三角形的性质进而求出$\frac{BE}{BC}$=$\frac{EF}{DC}$=$\frac{2}{5}$,求出EF即可.
解答 解:(1)△DFE与△DBA,△BFE与△BDC,△AEB与△DEC都是位似图形,
理由:∵AB∥CD∥EF,
∴△DFE∽△DBA,△BFE∽△BDC,△AEB∽△DEC,且对应边都交于一点,
∴△DFE与△DBA,△BFE与△BDC,△AEB与△DEC都是位似图形;
(2)∵△BFE∽△BDC,△AEB∽△DEC,AB=2,CD=3,
∴$\frac{AB}{DC}$=$\frac{BE}{EC}$=$\frac{2}{3}$,
∴$\frac{BE}{BC}$=$\frac{EF}{CD}$=$\frac{2}{5}$,
解得:EF=$\frac{6}{5}$.
点评 此题主要考查了比例的性质以及相似三角形的判定与性质,正确把握位似图形的定义是解题关键.

练习册系列答案
相关题目
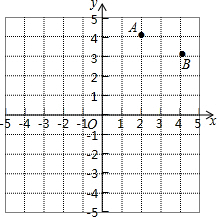 如图,有8×8的正方形网格,按要求操作并计算.
如图,有8×8的正方形网格,按要求操作并计算.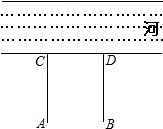 如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,且AC=BD.若A到河岸CD的中点的距离为500米.
如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,且AC=BD.若A到河岸CD的中点的距离为500米.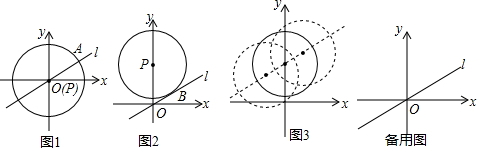
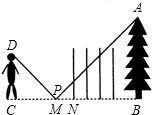 王明同学为了测量河对岸树AB的高度.他在河岸边放一面平面镜MN,他站在C处通过平面镜看到树的顶端A.如图,然后他量得B、P间的距离是56米,C、P间距离是12米,他的身高是1.74米.请你帮他计算出树AB的高度.
王明同学为了测量河对岸树AB的高度.他在河岸边放一面平面镜MN,他站在C处通过平面镜看到树的顶端A.如图,然后他量得B、P间的距离是56米,C、P间距离是12米,他的身高是1.74米.请你帮他计算出树AB的高度.