题目内容
20.先阅读下面的材料.再解答下面的问题.∵($\sqrt{a}$+$\sqrt{b}$)($\sqrt{a}$-$\sqrt{b}$)=a-b,
∴a-b=($\sqrt{a}$+$\sqrt{b}$)($\sqrt{a}$-$\sqrt{b}$)
特别地.($\sqrt{12}$+$\sqrt{11}$)×($\sqrt{12}$-$\sqrt{11}$)=1,
∴$\frac{1}{\sqrt{12}-\sqrt{11}}$=$\sqrt{12}$+$\sqrt{11}$,
当然也可以利用12-11=1得1=12-11,
故$\frac{1}{\sqrt{12}-\sqrt{11}}$=$\frac{(\sqrt{12})^2-(\sqrt{11})^2}{\sqrt{12}-\sqrt{11}}$=$\sqrt{12}+\sqrt{11}$
这种变形也是将分母有理化.
利用上述的思路方法解答下列问题:
(1)计算:$\frac{1}{3-\sqrt{8}}$-$\frac{1}{\sqrt{8}-\sqrt{7}}$+$\frac{1}{\sqrt{7}-\sqrt{6}}$-$\frac{1}{\sqrt{6}-\sqrt{5}}$+$\frac{1}{\sqrt{5}+2}$;
(2)计算:$\frac{5}{4-\sqrt{11}}$-$\frac{4}{\sqrt{11}-\sqrt{7}}$-$\frac{2}{3+\sqrt{7}}$.
分析 (1)先把每一部分分母有理化,化简后合并同类二次根式即可;
(2)先把每一部分分母有理化,化简后合并同类二次根式即可.
解答 解:(1)原式=$\frac{3+\sqrt{8}}{(3-\sqrt{8})(3+\sqrt{8})}$-$\frac{\sqrt{8}+\sqrt{7}}{(\sqrt{8}-\sqrt{7})(\sqrt{8}+\sqrt{7})}$+$\frac{\sqrt{7}+\sqrt{6}}{(\sqrt{7}-\sqrt{6})(\sqrt{7}+\sqrt{6})}$-$\frac{\sqrt{6}+\sqrt{5}}{(\sqrt{6}-\sqrt{5})(\sqrt{6}+\sqrt{5})}$+$\frac{\sqrt{5}-2}{(\sqrt{5}+2)(\sqrt{5}-2)}$
=3+$\sqrt{8}$-($\sqrt{8}$+$\sqrt{7}$)+$\sqrt{7}$+$\sqrt{6}$-($\sqrt{6}$+$\sqrt{5}$)+$\sqrt{5}$-2
=3-2
=1;
(2)原式=$\frac{5×(4+\sqrt{11})}{(4-\sqrt{11})(4+\sqrt{11})}$-$\frac{4×(\sqrt{11}+\sqrt{7})}{(\sqrt{11}-\sqrt{7})(\sqrt{11}+\sqrt{7})}$-$\frac{2×(3-\sqrt{7})}{(3+\sqrt{7})(3-\sqrt{7})}$
=4+$\sqrt{11}$-($\sqrt{11}$+$\sqrt{7}$)-(3-$\sqrt{7}$))
=4+$\sqrt{11}$-$\sqrt{11}$-$\sqrt{7}$-3+$\sqrt{7}$
=1.
点评 本题考查分母有理化的应用,能正确分母有理化因式时解此题的关键,难度适中.

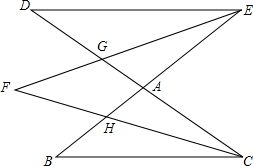 如图,DC和BE相交于点A,EF平分∠DEA,CF平分∠ACB,EF,CF分别与AD,AB交于点G,H,请猜想∠F与∠B,∠D之间的数量关系,并证明你的结论.
如图,DC和BE相交于点A,EF平分∠DEA,CF平分∠ACB,EF,CF分别与AD,AB交于点G,H,请猜想∠F与∠B,∠D之间的数量关系,并证明你的结论. 如图,在△ABC中,D是AB边上任意一点,连接CD.求证:AB+AC>DC+DB.
如图,在△ABC中,D是AB边上任意一点,连接CD.求证:AB+AC>DC+DB.