题目内容
10.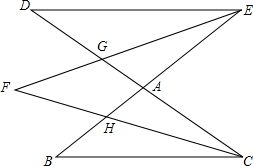 如图,DC和BE相交于点A,EF平分∠DEA,CF平分∠ACB,EF,CF分别与AD,AB交于点G,H,请猜想∠F与∠B,∠D之间的数量关系,并证明你的结论.
如图,DC和BE相交于点A,EF平分∠DEA,CF平分∠ACB,EF,CF分别与AD,AB交于点G,H,请猜想∠F与∠B,∠D之间的数量关系,并证明你的结论.
分析 根据角平分线的定义得到∠DEF=∠FEB和∠DCF=∠BCF,根据三角形的外角的性质计算得到答案.
解答 解:∠F=$\frac{1}{2}$(∠B+∠D).
证明:∵EF平分∠DEA,CF平分∠ACB,
∴∠DEF=∠FEB=$\frac{1}{2}$∠DEB,∠DCF=∠BCF=$\frac{1}{2}$∠DCB,
∠D+∠DEF=∠F+∠DCF①,
∠B+∠FCB=∠F+∠FEB②,
①+②得:2∠F=∠B+∠D,
∴∠F=$\frac{1}{2}$(∠B+∠D).
点评 本题考查的是三角形的外角的性质和角平分线的定义,掌握三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
20.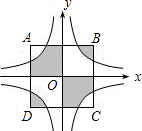 如图,正方形ABCD的边长为4,其中它的中心与原点重合,AB∥x轴,BC∥y轴,反比例函数y=$\frac{2}{x}$与y=-$\frac{2}{x}$的图象均与正方形ABCD的边相交,则图中阴影面积的和是( )
如图,正方形ABCD的边长为4,其中它的中心与原点重合,AB∥x轴,BC∥y轴,反比例函数y=$\frac{2}{x}$与y=-$\frac{2}{x}$的图象均与正方形ABCD的边相交,则图中阴影面积的和是( )
 如图,正方形ABCD的边长为4,其中它的中心与原点重合,AB∥x轴,BC∥y轴,反比例函数y=$\frac{2}{x}$与y=-$\frac{2}{x}$的图象均与正方形ABCD的边相交,则图中阴影面积的和是( )
如图,正方形ABCD的边长为4,其中它的中心与原点重合,AB∥x轴,BC∥y轴,反比例函数y=$\frac{2}{x}$与y=-$\frac{2}{x}$的图象均与正方形ABCD的边相交,则图中阴影面积的和是( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
18.某校七、八年级举行科普知识竞赛,两年级参赛人数相等.初赛共10道选择题,满分为100分.初赛结束后,经过统计绘制如下尚不完整的统计图表.
七年级成绩统计表

(1)在图1中,“100分”所在的扇形圆心角等于36°.
(2)请你将图2的统计图补充完整.
(3)经计算,八年级的平均分是80分、中位数是80分、请你写出七年级的平均分、中位数;并从平均分、中位数的角度分析哪个年级的成绩较好?
(4)若七、八年级各选3人参加复赛,请你分析,哪个年级的实力更强一些.
七年级成绩统计表
| 分数 | 70分 | 80分 | 90分 | 100分 |
| 人数 | 6 | 1 | 0 | 3 |

(1)在图1中,“100分”所在的扇形圆心角等于36°.
(2)请你将图2的统计图补充完整.
(3)经计算,八年级的平均分是80分、中位数是80分、请你写出七年级的平均分、中位数;并从平均分、中位数的角度分析哪个年级的成绩较好?
(4)若七、八年级各选3人参加复赛,请你分析,哪个年级的实力更强一些.
 函数y=kx+b的图象如图所示,试证明:关于x的一元二次方程x2+3x+k-1=0必有两个不等实根.
函数y=kx+b的图象如图所示,试证明:关于x的一元二次方程x2+3x+k-1=0必有两个不等实根.