题目内容
14．请你在横线上写一个无理数$\sqrt{2}$．分析 无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．
解答 解：无理数有$\sqrt{2}$（π等，答案不唯一）．
故答案是：$\sqrt{2}$．
点评 此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
2．
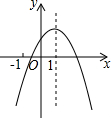如图，二次函数y=ax2+bx+c的图象的对称轴是直线x=1，则下列结论：
①a＜0，b＜0；②a+b+c＞0；③a-b+c＜0；④当x＞1时，y随x的增大而减小；
⑤b2-4ac＞0；⑥4a+2b+c＞0；⑦a+b＞m（am+b）（m≠1）．
其中正确的结论有（ ）
如图，二次函数y=ax2+bx+c的图象的对称轴是直线x=1，则下列结论：①a＜0，b＜0；②a+b+c＞0；③a-b+c＜0；④当x＞1时，y随x的增大而减小；
⑤b2-4ac＞0；⑥4a+2b+c＞0；⑦a+b＞m（am+b）（m≠1）．
其中正确的结论有（ ）
| A． | 4个 | B． | 5个 | C． | 6个 | D． | 7个 |
6．移动互联网已经全面进入人们的日常生活，截止2015年3月，全国4G用户总数达到162000000，其中162000000用科学记数法表示为（ ）
| A． | 1.62×104 | B． | 1.62×106 | C． | 1.62×108 | D． | 0.162×109 |
3．
如图，A点的坐标为（2，3），则tan∠AOy的值是（ ）
如图，A点的坐标为（2，3），则tan∠AOy的值是（ ）| A． | $\frac{2}{3}$ | B． | $\frac{3}{2}$ | C． | $\frac{{2\sqrt{13}}}{13}$ | D． | $\frac{{3\sqrt{13}}}{13}$ |
如图，由边长相同的小正方形组成的网格图形，A、B、C都在格点上．