题目内容
2.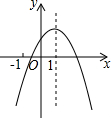 如图,二次函数y=ax2+bx+c的图象的对称轴是直线x=1,则下列结论:
如图,二次函数y=ax2+bx+c的图象的对称轴是直线x=1,则下列结论:①a<0,b<0;②a+b+c>0;③a-b+c<0;④当x>1时,y随x的增大而减小;
⑤b2-4ac>0;⑥4a+2b+c>0;⑦a+b>m(am+b)(m≠1).
其中正确的结论有( )
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
分析 由抛物线的开口方向判断a与0的关系,由抛物线与x轴的交点得出b2-4ac的符号,然后根据抛物线与x轴交点的个数及x=1时二次函数的值的情况进行推理,进而对所得结论进行判断.
解答 解:①∵抛物线开口向下,∴a<0,
∵抛物线对称轴为直线x=1,且a<0,
∴b>0,故此选项错误;
②当x=1时,对应y的值大于0,即a+b+c>0,故此选项正确;
③当x=-1时,对应y的值小于0,即a-b+c<0,故此选项正确;
④当x>1时,y随x的增大而减小,正确;
⑤图象与x轴有两个交点,故b2-4ac>0,正确;
⑥∵抛物线对称轴为直线x=1,且图象与x轴左侧交点大于-1,故抛物线与x轴右侧交点大于2,
故当x=2时4a+2b+c>0,正确;
⑦∵当x=1时,y最大,即a+b+c最大,故a+b+c>am2+bm+c,即a+b>m(am+b),(m为实数且m≠1),故此选项正确;
故正确的有6个.
故选:C.
点评 此题主要考查了图象与二次函数系数之间的关系,二次函数与方程之间的转换,会利用特殊值代入法求得特殊的式子,如:y=a+b+c,然后根据图象判断其值.

练习册系列答案
相关题目
10.下列方程是一元二次方程的是( )
| A. | x2-6x+2 | B. | 2x2-y+1=0 | C. | 5x2=0 | D. | $\frac{1}{{x}^{2}}$+x=2 |
17. 某校一间阶梯教室,第1排的座位数为12,从第2排开始,每一排都比前一排增加a个座位.
某校一间阶梯教室,第1排的座位数为12,从第2排开始,每一排都比前一排增加a个座位.
(1)请在下表的空格里填写一个适当的代数式.
(2)已知第15排座位数是第5排座位数的2倍,列方程为12+14a=2(12+4a).
 某校一间阶梯教室,第1排的座位数为12,从第2排开始,每一排都比前一排增加a个座位.
某校一间阶梯教室,第1排的座位数为12,从第2排开始,每一排都比前一排增加a个座位.(1)请在下表的空格里填写一个适当的代数式.
| 第1排 座位数 | 第2排 座位数 | 第3排 座位数 | 第4排 座位数 | … | 第n排 座位数 |
| 12 | 12+a | 12+2a | 12+3a | … | 12+(n-1)a |
12.下列计算正确的是( )
| A. | -(-2)3=8 | B. | -2-1=-1 | C. | 3÷$\frac{1}{3}$×3=3 | D. | (-2)4=8 |
 如图,EF⊥BC,AD⊥BC,∠1=∠2,∠BAC=80°.求∠AGD的度数.
如图,EF⊥BC,AD⊥BC,∠1=∠2,∠BAC=80°.求∠AGD的度数. 为了给草坪喷水,安装了自动旋转喷水器,如图所示.设直线AD所在位置为地平面,喷水管AB高出地平面1.5m,在B处有一个自动旋转的喷水头,一瞬间喷出的水流呈抛物线状.喷头B与水流最高点C的连线与地平面成45°的角,水流的最高点C离地平面3.5m,水流的落地点为D.在建立如图所示的直角坐标系中:
为了给草坪喷水,安装了自动旋转喷水器,如图所示.设直线AD所在位置为地平面,喷水管AB高出地平面1.5m,在B处有一个自动旋转的喷水头,一瞬间喷出的水流呈抛物线状.喷头B与水流最高点C的连线与地平面成45°的角,水流的最高点C离地平面3.5m,水流的落地点为D.在建立如图所示的直角坐标系中: