题目内容
7.已知m,n是两个不同的有理数,且满足(m+a)(m+b)-4=0,(n+a)(n+b)-4=0,则(m+a)(n+a)的值是-4.分析 把已知条件变形得到m2+(a+b)m+ab-4=0,n2+(a+b)n+ab-4=0,则可把m、n看作方程x2+(a+b)x+ab-4=0的两根,根据根与系数的关系得到m+n=-(a+b),mn=ab-4,
接着把(m+a)(n+a)展开整理得mn+a(m+n)+a2,然后利用整体代入的方法计算.
解答 解:∵(m+a)(m+b)-4=0,(n+a)(n+b)-4=0,
∴m2+(a+b)m+ab-4=0,n2+(a+b)n+ab-4=0,
m、n可看作方程x2+(a+b)x+ab-4=0的两根,
∴m+n=-(a+b),mn=ab-4,
∴(m+a)(n+a)=mn+a(m+n)+a2=ab-4-a•(a+b)+a2=ab-4-a2-ab+b2=-4.
故答案为-4.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
12.下列y与x之间的关系式:①y=-x;②y=3x-1;③y=2x2;④y=$\frac{1}{x}$,其中一次函数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
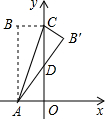 如图,矩形ABCO中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB′C,AB′交y轴于D点,则B′点的坐标为($\frac{42}{29}$,$\frac{105}{29}$).
如图,矩形ABCO中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB′C,AB′交y轴于D点,则B′点的坐标为($\frac{42}{29}$,$\frac{105}{29}$).