题目内容
13．
如图，将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上．如果∠2=60°，那么∠1的度数为30°．
分析 根据三角形外角性质可得∠3=30°+∠1，由平行线的性质即可得到∠2=∠3=60°，即可解答．
解答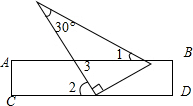 
解：如图，
∵∠3=∠1+30°，
∵AB∥CD，
∴∠2=∠3=60°，
∴∠1=∠3-30°=60°-30°=30°．
故答案为：30°．
点评 本题考查了平行线的性质，关键是根据：两直线平行，内错角相等．也利用了三角形外角性质．
练习册系列答案
相关题目
3．“任意买一张电影票，座位号是奇数”，此事件是（ ）
| A． | 不可能事件 | B． | 不确定事件 | C． | 必然事件 | D． | 确定事件 |
8．化简（$\frac{2a}{5{a}^{2}b}+\frac{3b}{10a{b}^{2}}$）÷$\frac{7}{2{a}^{3}{b}^{2}}$的结果为（ ）
| A． | $\frac{7}{{a}^{2}b}$ | B． | $\frac{7{a}^{2}b}{10}$ | C． | $\frac{{a}^{2}b}{5}$ | D． | $\frac{10}{7{a}^{2}b}$ |
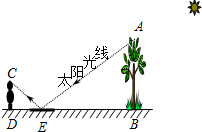如图，为了测量校园内一棵不可攀的树的高度，数学应用实践小组做了如下的探索实践：根据《物理学》中光的反射定律，利用一面镜子和一根皮尺，设计如图的测量方案：把镜子放在离树（AB）9米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到树梢顶点A，再用皮尺量得DE=2.7米，观察者目高CD=1.8米，则树（AB）的高度为6米．
2．下列运算不正确的是（ ）
| A． | 当a≥0时，$\sqrt{{a}^{2}}$=a | B． | $\root{3}{{a}^{3}}$=a | C． | 当a＜0时，$\sqrt{{a}^{2}}$=-a | D． | $\sqrt{（-9）^{2}}$=-9 |