题目内容
18.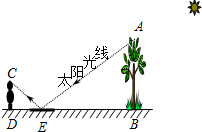 如图,为了测量校园内一棵不可攀的树的高度,数学应用实践小组做了如下的探索实践:根据《物理学》中光的反射定律,利用一面镜子和一根皮尺,设计如图的测量方案:把镜子放在离树(AB)9米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者目高CD=1.8米,则树(AB)的高度为6米.
如图,为了测量校园内一棵不可攀的树的高度,数学应用实践小组做了如下的探索实践:根据《物理学》中光的反射定律,利用一面镜子和一根皮尺,设计如图的测量方案:把镜子放在离树(AB)9米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者目高CD=1.8米,则树(AB)的高度为6米.
分析 因为入射光线和反射光线与镜面的夹角相等且人和树均垂直于地面,所以构成两个相似三角形,利用相似比即可求出.
解答 解:∵∠CED=∠AEB,CD⊥DB,AB⊥BD,
∴△CED∽△AEB,
∴$\frac{CD}{AB}$=$\frac{DE}{BE}$,
又∵CD=1.8,DE=2.7,BE=9,
∴$\frac{1.8}{AB}$=$\frac{2.7}{9}$,
∴AB=6.
故答案为6.
点评 本题考查了相似三角形的应用,关键要找准对应线段,要和物理知识相联系,知道入射光线和反射光线与镜面的夹角相等.

练习册系列答案
相关题目
8.下列命题,是真命题的是( )
| A. | 已知P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2013的值是1 | |
| B. | 甲乙两组数据的平均数相等,且S甲2>S乙2,则甲比乙稳定 | |
| C. | 两边长分别为12、10的等腰△ABC底边上的高等于8 | |
| D. | 若$\sqrt{{a}^{2}}$=-a,则实数a一定不在数轴原点右侧 |
6.下列图形中,可以看做是轴对称图形的是( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.二次函数y=a(x-1)2+k(a>0)中x、y的几组对应值如下表.
表中m、n、p的大小关系为n<m<p(用“<”连接)
| x | -2 | 1 | 5 |
| y | m | n | p |
8.2014第二届中国(绵阳)科技城国际博览会科技部、国家知识产权局、国家国防科工局和四川省人民政府共同主办,于2014年10月16日至18日在中国科技城-四川省绵阳市落幕,记者从大会组委会获悉,本届科博会签约项目945个,金额达883.6亿元,把883.6亿元用科学记数法表示为( )
| A. | 883.6×108元 | B. | 8.836×109元 | C. | 8.836×1010元 | D. | 8.836×1011元 |
 如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.如果∠2=60°,那么∠1的度数为30°.
如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.如果∠2=60°,那么∠1的度数为30°.