题目内容
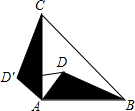 如图,D是等腰直角三角形ABC内一点,BC是斜边,如果将△ABD绕点A按逆时针方向旋转到△ACD′的位置,则∠DAD′的度数是
如图,D是等腰直角三角形ABC内一点,BC是斜边,如果将△ABD绕点A按逆时针方向旋转到△ACD′的位置,则∠DAD′的度数是考点:旋转的性质
专题:
分析:先由等腰直角三角形的性质得出∠BAC=90°,再根据对应点与旋转中心所连线段的夹角等于旋转角即可作答.
解答:解:∵D是等腰直角三角形ABC内一点,BC是斜边,
∴∠BAC=90°,
∵将△ABD绕点A按逆时针方向旋转到△ACD′的位置,
∴∠DAD′=∠BAC=90°.
故答案为90°.
∴∠BAC=90°,
∵将△ABD绕点A按逆时针方向旋转到△ACD′的位置,
∴∠DAD′=∠BAC=90°.
故答案为90°.
点评:本题考查旋转的性质:对应点与旋转中心所连线段的夹角等于旋转角;旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.要注意旋转的三要素:①定点为旋转中心;②旋转方向;③旋转角度.

练习册系列答案
相关题目
 下列图形中,既是轴对称图形又是中心对称图形的共有( )个.
下列图形中,既是轴对称图形又是中心对称图形的共有( )个.| A、1 | B、2 | C、3 | D、4 |
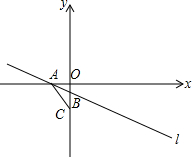 如图,已知直线l:y=-
如图,已知直线l:y=-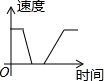
 已知△ABC和△ADE中,AB=BC,AD=DE,∠ABC=∠ADE=90°,连接CE,M为中点,连接DM,BM.求证:
已知△ABC和△ADE中,AB=BC,AD=DE,∠ABC=∠ADE=90°,连接CE,M为中点,连接DM,BM.求证: