题目内容
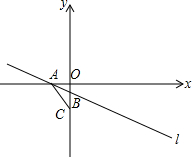 如图,已知直线l:y=-
如图,已知直线l:y=-| 1 |
| 2 |
| ||
| 5 |
(1)求点C的坐标;
(2)若∠CDB=∠ACB,求抛物线的解析式;
(3)在(2)的条件下,当a>0时,若点P是直线l下方的抛物线上一动点(不与A、D重合),过点P作PM⊥AD于点M,并设点P的横坐标为m,用含m的代数式表示线段PM的长,并求出线段PM的最大值.
考点:一次函数综合题
专题:
分析:(1)根据自变量的值,可得相应的函数值,根据正弦函数,可得AC的长,根据勾股定理,可得答案;
(2)根据三角形的面积公式,可得CE的长,根据等角的三角函数值相等,可得CD的值,根据两点间的距离,可得D点坐标,根据待定系数法,可得答案;
(3)根据点到直线的距离公式,可得用含m的代数式表示线段PM的长,根据负数越小绝对值越大,可得答案.
(2)根据三角形的面积公式,可得CE的长,根据等角的三角函数值相等,可得CD的值,根据两点间的距离,可得D点坐标,根据待定系数法,可得答案;
(3)根据点到直线的距离公式,可得用含m的代数式表示线段PM的长,根据负数越小绝对值越大,可得答案.
解答:解:如图:
(1)当y=0时,-
x-1=0,解得x=-2,即A(-2,0),
当x=0时,y=-1,即B(0,-1).
sin∠ACB=
=
=
,解得AC=2
,
由勾股定理,得
OC=
=
=4,
C点坐标是(0,-4);
(2)作CE⊥AD,
S△ABC=
AB•CE=S△AOC-S△AOB,
•CE=
×2×4-
×2×1,
解得CE=
.
由∠CDB=∠ACB,得
sin∠CDB=
=sin∠ACB=
,
解得CD=6.
设D点坐标是(x,-
x-1),
由CD=6,得
x2+(-
x-1+42=62,
解得x1=-
(不符合题意的要舍去),x2=6,
把x=6代入y=-
x-1,得y=-4,即D(6,-4).
当A(-2,0),C(0,-4),D(6,-4)在函数图象上,
得
,解得
,
抛物线的解析式为y=
x2-2x-4;
(3)设P点坐标为(m,
m2-2m-4),由点到直线的距离公式,得
PM=
=
=||
m2-3m-6|×
,
PM最大=|
×(
)2-
×
-3|×
=
.

(1)当y=0时,-
| 1 |
| 2 |
当x=0时,y=-1,即B(0,-1).
sin∠ACB=
| AO |
| AC |
| 2 |
| AC |
| ||
| 5 |
| 5 |
由勾股定理,得
OC=
| AC2-AO2 |
| 20-4 |
C点坐标是(0,-4);
(2)作CE⊥AD,
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
解得CE=
6
| ||
| 5 |
由∠CDB=∠ACB,得
sin∠CDB=
| CE |
| CD |
| ||
| 5 |
解得CD=6.
设D点坐标是(x,-
| 1 |
| 2 |
由CD=6,得
x2+(-
| 1 |
| 2 |
解得x1=-
| 18 |
| 5 |
把x=6代入y=-
| 1 |
| 2 |
当A(-2,0),C(0,-4),D(6,-4)在函数图象上,
得
|
|
抛物线的解析式为y=
| 1 |
| 3 |
(3)设P点坐标为(m,
| 1 |
| 3 |
PM=
|
| ||||
|
2|
| ||||
|
| 2 |
| 3 |
| ||
| 5 |
PM最大=|
| 2 |
| 3 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| ||
| 5 |
| 225 |
| 16 |
点评:本题考查了一次函数综合题,(1)利用了三角函数,勾股定理,(2)利用了等角三角函数的关系,利用了待定系数法求解析式,(3)利用了点到直线的距离公式.

练习册系列答案
相关题目
水星和太阳的平均距离约为57900000km,用科学记数法表示为( )
| A、57.9×106km |
| B、0.579×108km |
| C、5.79×107km |
| D、5.79×108 |
 如图,两条平行线a、b被直线c所截.若∠1=115°,则∠2=
如图,两条平行线a、b被直线c所截.若∠1=115°,则∠2= 如图,在梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,AD=1,BC=4,E为AB中点,EF∥DC交BC于点F,
如图,在梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,AD=1,BC=4,E为AB中点,EF∥DC交BC于点F, 如图,D是等腰直角三角形ABC内一点,BC是斜边,如果将△ABD绕点A按逆时针方向旋转到△ACD′的位置,则∠DAD′的度数是
如图,D是等腰直角三角形ABC内一点,BC是斜边,如果将△ABD绕点A按逆时针方向旋转到△ACD′的位置,则∠DAD′的度数是 如图,等腰△ABC的底边在y轴正半轴上,顶点C在第一象限,延长AC交双曲线y=
如图,等腰△ABC的底边在y轴正半轴上,顶点C在第一象限,延长AC交双曲线y=