题目内容
“端午节”是我国的传统佳节,历来有吃“粽子”的习俗.我市某食品加工厂,拥有两条不同粽子加工生产线A、B.原计划A生产线每小时加工粽子400个,B生产线每小时加工粽子500个.
(1)若生产线A、B一共工作12小时,且生产粽子总数量不少于5500个,则B生产线至少加工生产多少小时?
(2)原计划A、B生产线每天均工作8小时,由于受其他原因影响,在实际生产过程中,A生产线每小时比原计划少生产100a个(a>0),B生产线每小时比原计划少生产100个.为了尽快将粽子投放到市场,A生产线每天比原计划多工作2a小时,B生产线每天比原计划多工作a小时.这样一天恰好生产粽子6400个,求a的值.
(1)若生产线A、B一共工作12小时,且生产粽子总数量不少于5500个,则B生产线至少加工生产多少小时?
(2)原计划A、B生产线每天均工作8小时,由于受其他原因影响,在实际生产过程中,A生产线每小时比原计划少生产100a个(a>0),B生产线每小时比原计划少生产100个.为了尽快将粽子投放到市场,A生产线每天比原计划多工作2a小时,B生产线每天比原计划多工作a小时.这样一天恰好生产粽子6400个,求a的值.
考点:一元二次方程的应用,一元一次不等式的应用
专题:
分析:(1)设B生产线至少加工生产x小时,则A生产线加工生产(12-x)小时,根据生产粽子总数量不少于5500个,列出不等式解决问题;
(2)利用A、B生产的总数量的和是6400个列出方程解决问题.
(2)利用A、B生产的总数量的和是6400个列出方程解决问题.
解答:解:(1)设B生产线至少加工生产x小时,则A生产线加工生产(12-x)小时,由题意得
500x+400(12-x)≥5500
解得x≥7
答:B生产线至少加工生产7小时.
(2)由题意得
(400-100a)(8+2a)+(500-100)(8+a)=6400
整理得-2a2+4a=0,
解得a1=2,a2=-2(不合题意舍去)
答:a的值是2.
500x+400(12-x)≥5500
解得x≥7
答:B生产线至少加工生产7小时.
(2)由题意得
(400-100a)(8+2a)+(500-100)(8+a)=6400
整理得-2a2+4a=0,
解得a1=2,a2=-2(不合题意舍去)
答:a的值是2.
点评:此题考查一元一次不等式,一元二次方程的实际运用,找出题目蕴含的数量关系,列出方程或不等式解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
水星和太阳的平均距离约为57900000km,用科学记数法表示为( )
| A、57.9×106km |
| B、0.579×108km |
| C、5.79×107km |
| D、5.79×108 |
有甲、乙两块铁板(厚度忽略不计),甲的形状为直角梯形,两底边长分别为4cm,10cm,且有一内角为60°;乙的形状为等腰三角形,其顶角为45°,腰长12cm.在不改变形状的前提下,试图分别把它们从一个直径为8.7cm的圆洞中穿过,结果是( )
| A、甲板能穿过,乙板不能穿过 |
| B、甲板不能穿过,乙板能穿过 |
| C、甲、乙两板都能穿过 |
| D、甲、乙两板都不能穿过 |
函数y=ax+a与y=
(a≠0)在同一直角坐标系中的图象可能是( )
| a |
| x |
A、 |
B、 |
C、 |
D、 |
 如图,在梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,AD=1,BC=4,E为AB中点,EF∥DC交BC于点F,
如图,在梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,AD=1,BC=4,E为AB中点,EF∥DC交BC于点F,
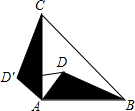 如图,D是等腰直角三角形ABC内一点,BC是斜边,如果将△ABD绕点A按逆时针方向旋转到△ACD′的位置,则∠DAD′的度数是
如图,D是等腰直角三角形ABC内一点,BC是斜边,如果将△ABD绕点A按逆时针方向旋转到△ACD′的位置,则∠DAD′的度数是 如图,与∠1是同位角的角是
如图,与∠1是同位角的角是