题目内容
点A、B、C在数轴上表示的数a、b、c满足:(b+2)2+(c-24)2=0,且多项式x|a+3|y2一ax3y+xy2-1是五次四项式.
(1)则a的值为 ,b的值为 ,c的值为
(2)若数轴上有三个动点M、N、P,分别从点A、B、C开始同时出发,在数轴上运动,速度分别为每秒1个单位长度、7个单位长度、3个单位长度,其中点P向左运动,点N先向左运动,遇到点M 后回头再向右运动,遇到点P后回头向左运动,…,这样直到点P遇到点M时三点都停止运动,求点N所走的路程.
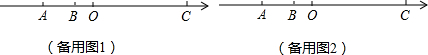
(3)点D为数轴上一点,它表示的数为x,求:
(3x-a)2+(x-b)2--
(-12x-c)2+4的最大值,并回答这时x的值是多少.
(1)则a的值为
(2)若数轴上有三个动点M、N、P,分别从点A、B、C开始同时出发,在数轴上运动,速度分别为每秒1个单位长度、7个单位长度、3个单位长度,其中点P向左运动,点N先向左运动,遇到点M 后回头再向右运动,遇到点P后回头向左运动,…,这样直到点P遇到点M时三点都停止运动,求点N所走的路程.
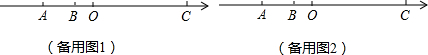
(3)点D为数轴上一点,它表示的数为x,求:
| 49 |
| 81 |
| 1 |
| 16 |
考点:数轴,非负数的性质:偶次方,多项式
专题:计算题
分析:(1)利用非负数的性质求出b与c的值,根据多项式为五次四项式求出a的值;
(2)由题意只要求出点P遇到点M的时间,也就是点N的运动时间,首先求出AC的距离,设相遇时间为t,分别表示出两点行驶的距离,建立方程解决问题;
(3)把a、b、c三点代入,利用公式法求出答案即可.
(2)由题意只要求出点P遇到点M的时间,也就是点N的运动时间,首先求出AC的距离,设相遇时间为t,分别表示出两点行驶的距离,建立方程解决问题;
(3)把a、b、c三点代入,利用公式法求出答案即可.
解答:解:(1)∵(b+2)2+(c-24)2=0,
∴b=-2,c=24,
∵多项式x|a+3|y2一ax3y+xy2-1是五次四项式,
∴|a+3|=5-2,-a≠0,
∴a=-6;
(2)AC=24-(-6)=30,
设经过t秒点P遇到点M,
则t+3t=30,
解得t=7.5,
点N所走的路程为7×7.5=52.5个单位长度,
答:点N所走的路程为52.5个单位长度;
(3)把a=-6,b=-2,c=24代入得,
(3x-a)2+(x-b)2-
(-12x-c)2+4
=
(3x+6)2+(x+2)2-
(-12x-24)2+4
=-
x2-
x-
,
当x=-
=-
时,最大值为
=
=
.
∴b=-2,c=24,
∵多项式x|a+3|y2一ax3y+xy2-1是五次四项式,
∴|a+3|=5-2,-a≠0,
∴a=-6;
(2)AC=24-(-6)=30,
设经过t秒点P遇到点M,
则t+3t=30,
解得t=7.5,
点N所走的路程为7×7.5=52.5个单位长度,
答:点N所走的路程为52.5个单位长度;
(3)把a=-6,b=-2,c=24代入得,
| 49 |
| 81 |
| 1 |
| 16 |
=
| 49 |
| 81 |
| 1 |
| 16 |
=-
| 23 |
| 9 |
| 132 |
| 9 |
| 96 |
| 9 |
当x=-
-
| ||
2×(-
|
| 66 |
| 23 |
4×(-
| ||||||
4×(-
|
| 8592 |
| 828 |
| 716 |
| 69 |
点评:本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解;注意根据二次函数的性质利用公式法求最大值的理解掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,D,E分别是△ABC的边AB,AC上的点,DE∥BC,若
如图,D,E分别是△ABC的边AB,AC上的点,DE∥BC,若| AD |
| DB |
| 2 |
| 3 |
| DE |
| BC |
A、
| ||
B、
| ||
C、
| ||
D、
|
有甲、乙两块铁板(厚度忽略不计),甲的形状为直角梯形,两底边长分别为4cm,10cm,且有一内角为60°;乙的形状为等腰三角形,其顶角为45°,腰长12cm.在不改变形状的前提下,试图分别把它们从一个直径为8.7cm的圆洞中穿过,结果是( )
| A、甲板能穿过,乙板不能穿过 |
| B、甲板不能穿过,乙板能穿过 |
| C、甲、乙两板都能穿过 |
| D、甲、乙两板都不能穿过 |
 如图,在梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,AD=1,BC=4,E为AB中点,EF∥DC交BC于点F,
如图,在梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,AD=1,BC=4,E为AB中点,EF∥DC交BC于点F,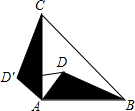 如图,D是等腰直角三角形ABC内一点,BC是斜边,如果将△ABD绕点A按逆时针方向旋转到△ACD′的位置,则∠DAD′的度数是
如图,D是等腰直角三角形ABC内一点,BC是斜边,如果将△ABD绕点A按逆时针方向旋转到△ACD′的位置,则∠DAD′的度数是 如图,与∠1是同位角的角是
如图,与∠1是同位角的角是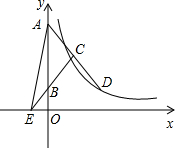 如图,等腰△ABC的底边在y轴正半轴上,顶点C在第一象限,延长AC交双曲线y=
如图,等腰△ABC的底边在y轴正半轴上,顶点C在第一象限,延长AC交双曲线y=