题目内容
观察下面的表格.
(1)求a、b、c的值;
(2)设y=ax2+bx+c,求这个二次函数图象的对称轴和图象与x轴的交点坐标.
| x | 0 | 1 | 2 |
| ax2 | 1 | ||
| ax2+bx+c | -3 | -3 |
(2)设y=ax2+bx+c,求这个二次函数图象的对称轴和图象与x轴的交点坐标.
考点:二次函数的性质
专题:图表型
分析:(1)根据表格中的三组对应值,根据二次函数图象上点的坐标特征可分别求出a、b、c的值;
(2)由(1)得到二次函数解析式,再配成顶点式得到对称轴,然后求函数值为0所对应的自变量的值即可得到二次函数图象图象与x轴的交点坐标.
(2)由(1)得到二次函数解析式,再配成顶点式得到对称轴,然后求函数值为0所对应的自变量的值即可得到二次函数图象图象与x轴的交点坐标.
解答:解:(1)把(1,1)y=ax2得a=1;
把(0,-3),(2,-3)代入y=x2+bx+c得
,解得
;
(2)二次函数解析式为y=x2-2x-3=(x-1)2-4,
所以而次函数图形的对称轴为直线x=1;
因为x2-2x-3=0的解为x1=-1,x2=3,
所以二次函数图象与x轴的交点坐标为(-1,0)和(3,0).
把(0,-3),(2,-3)代入y=x2+bx+c得
|
|
(2)二次函数解析式为y=x2-2x-3=(x-1)2-4,
所以而次函数图形的对称轴为直线x=1;
因为x2-2x-3=0的解为x1=-1,x2=3,
所以二次函数图象与x轴的交点坐标为(-1,0)和(3,0).
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,D,E分别是△ABC的边AB,AC上的点,DE∥BC,若
如图,D,E分别是△ABC的边AB,AC上的点,DE∥BC,若| AD |
| DB |
| 2 |
| 3 |
| DE |
| BC |
A、
| ||
B、
| ||
C、
| ||
D、
|
有甲、乙两块铁板(厚度忽略不计),甲的形状为直角梯形,两底边长分别为4cm,10cm,且有一内角为60°;乙的形状为等腰三角形,其顶角为45°,腰长12cm.在不改变形状的前提下,试图分别把它们从一个直径为8.7cm的圆洞中穿过,结果是( )
| A、甲板能穿过,乙板不能穿过 |
| B、甲板不能穿过,乙板能穿过 |
| C、甲、乙两板都能穿过 |
| D、甲、乙两板都不能穿过 |
某校共1380人参加中考,为了考查这1380名学生的外语成绩,从中抽取了80名学生的外语成绩进行调查,以下说法正确的是( )
| A、某校1380名学生的成绩是总体 |
| B、样本容量是80人 |
| C、其中80名学生的外语成绩是总体的一个样本 |
| D、每个学生是个体 |
下列计算正确的是( )
| A、a2+a2=2a2 |
| B、a3•a2=a6 |
| C、a6÷a3=a2 |
| D、(3a)3=9 |
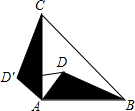 如图,D是等腰直角三角形ABC内一点,BC是斜边,如果将△ABD绕点A按逆时针方向旋转到△ACD′的位置,则∠DAD′的度数是
如图,D是等腰直角三角形ABC内一点,BC是斜边,如果将△ABD绕点A按逆时针方向旋转到△ACD′的位置,则∠DAD′的度数是
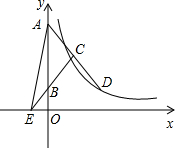 如图,等腰△ABC的底边在y轴正半轴上,顶点C在第一象限,延长AC交双曲线y=
如图,等腰△ABC的底边在y轴正半轴上,顶点C在第一象限,延长AC交双曲线y=