题目内容
 已知△ABC和△ADE中,AB=BC,AD=DE,∠ABC=∠ADE=90°,连接CE,M为中点,连接DM,BM.求证:
已知△ABC和△ADE中,AB=BC,AD=DE,∠ABC=∠ADE=90°,连接CE,M为中点,连接DM,BM.求证:(1)DM=BM;
(2)BM⊥DM.
考点:全等三角形的判定与性质,等腰直角三角形
专题:证明题
分析:(1)延长BM至点N,使MN=BM,连接DB,DN,NE,延长NE交AB于F,证△EMN≌△CMB,推出EN=CB,∠ENM=∠CBM,求出EN=AB,EN⊥AB,∠DEN=∠DAF,证△DAB≌△DEN,推出DN=DB,∠ADB=∠EDN,推出△BDN为等腰直角三角形,即可得出答案;
(2)根据等腰三角形的性质得出即可.
(2)根据等腰三角形的性质得出即可.
解答:(1)证明:延长BM至点N,使MN=BM,连接DB,DN,NE,延长NE交AB于F,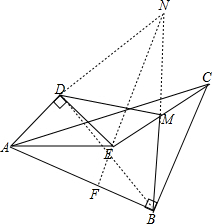
∵在△EMN和△CMB中
∴△EMN≌△CMB,
∴EN=CB,∠ENM=∠CBM,
∴EN∥CB,
∵AB=BC,AB⊥CB,
∴EN=AB,EN⊥AB,
∵∠ADE=90°,EN⊥AB,
在四边形ADEF中,∠DAF+∠DEF=180°,∠DEN+∠DEF=180°,
∴∠DEN=∠DAF,
在△DAB和△DEN中
∴△DAB≌△DEN,
∴DN=DB,∠ADB=∠EDN,
∴∠BDN=∠ADE=90°,
∴△BDN为等腰直角三角形,
∴DM=BM;
(2)∵△BDN为等腰直角三角形,
∴DM⊥BM.

∵在△EMN和△CMB中
|
∴△EMN≌△CMB,
∴EN=CB,∠ENM=∠CBM,
∴EN∥CB,
∵AB=BC,AB⊥CB,
∴EN=AB,EN⊥AB,
∵∠ADE=90°,EN⊥AB,
在四边形ADEF中,∠DAF+∠DEF=180°,∠DEN+∠DEF=180°,
∴∠DEN=∠DAF,
在△DAB和△DEN中
|
∴△DAB≌△DEN,
∴DN=DB,∠ADB=∠EDN,
∴∠BDN=∠ADE=90°,
∴△BDN为等腰直角三角形,
∴DM=BM;
(2)∵△BDN为等腰直角三角形,
∴DM⊥BM.
点评:本题考查了等腰直角三角形的性质和判定,全等三角形的性质和判定,等腰三角形的性质的应用,题目比较典型,综合性比较强,难度偏大.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 如图,D,E分别是△ABC的边AB,AC上的点,DE∥BC,若
如图,D,E分别是△ABC的边AB,AC上的点,DE∥BC,若| AD |
| DB |
| 2 |
| 3 |
| DE |
| BC |
A、
| ||
B、
| ||
C、
| ||
D、
|
 化简并求值:
化简并求值: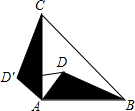 如图,D是等腰直角三角形ABC内一点,BC是斜边,如果将△ABD绕点A按逆时针方向旋转到△ACD′的位置,则∠DAD′的度数是
如图,D是等腰直角三角形ABC内一点,BC是斜边,如果将△ABD绕点A按逆时针方向旋转到△ACD′的位置,则∠DAD′的度数是 如图,在△ABC中,点P是△ABC的外角∠DBC、∠BCE的平分线的交点,若∠BPC=70°,则∠BAC=
如图,在△ABC中,点P是△ABC的外角∠DBC、∠BCE的平分线的交点,若∠BPC=70°,则∠BAC=