题目内容
3. △ABC在平面直角坐标系中的位置如图所示:
△ABC在平面直角坐标系中的位置如图所示:(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以原点O为位似中心,在y轴左侧将△A1B1C1放大为原来的2倍,得到的△A2B2C2,请画出△A2B2C2;
(3)设P(x,y)为△ABC内任意一点,△A2B2C2内的点P′是点P经过上述两次变换后的对应点,请直接写出P′的坐标.
分析 (1)根据关于x轴对称的点的坐标特征写出A1、B1、C1的坐标,然后描点即可得到△A1B1C1;
(2)在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k,则把A、B、C的横纵坐标分别乘以-2得到A2、B2、C2的坐标,然后描点即可得到△A2B2C2;
(3)把P点的横纵坐标分别乘以-2即可得到P′的坐标.
解答 解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;
(3)P′的坐标为(-2x,-2y).
点评 本题考查了作图-位似变换:先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;接着根据位似比,确定能代表所作的位似图形的关键点;然后顺次连接上述各点,得到放大或缩小的图形.也考查了轴对称变换.

练习册系列答案
相关题目
13.“十•一”期间,我市某生态公园在7天中每天游客的人数变化如表(正数表示比前一天多的人数,负数表示比前一天少的人数)
(1)若9月30日的游客人数记为a万人,请用含有a的式子表示10月2日的游客人数?
(2)请判断七天内游客人数最多的是哪天?请说明理由.
(3)建生态公园的目的一般有两个,一方面是给广大市民提供一个休闲游玩的好去处;另一方面是拉动内需,促进消费.若9月30日的游客人数为1万人,进园的人每人平均消费100元.问“十•一”期间所有的游园人员在生态园的总消费是多少万元?
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 人数变化 单位:万人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(2)请判断七天内游客人数最多的是哪天?请说明理由.
(3)建生态公园的目的一般有两个,一方面是给广大市民提供一个休闲游玩的好去处;另一方面是拉动内需,促进消费.若9月30日的游客人数为1万人,进园的人每人平均消费100元.问“十•一”期间所有的游园人员在生态园的总消费是多少万元?
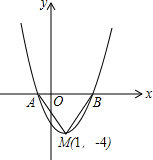 如图是二次函数y=(x-1)2-4的图象,与x轴交于A,B两点.将二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b(b<1)与此图象有两个公共点时,b的取值范围.
如图是二次函数y=(x-1)2-4的图象,与x轴交于A,B两点.将二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b(b<1)与此图象有两个公共点时,b的取值范围. 如图,在长度为1个单位长度的小正方形组成的长方形中,点A,B,C在小正方形的顶点上.
如图,在长度为1个单位长度的小正方形组成的长方形中,点A,B,C在小正方形的顶点上. 点F为?ABCD中DC边上的点,连接AF并延长交BC的延长线于E点,并且交BD于G,求证:AG2=FG•EG.
点F为?ABCD中DC边上的点,连接AF并延长交BC的延长线于E点,并且交BD于G,求证:AG2=FG•EG. 如图,抛物线y=x2+bx+c与x轴交A(-1、0)、B(3,0)两点,与y轴交于点C,顶点为D.
如图,抛物线y=x2+bx+c与x轴交A(-1、0)、B(3,0)两点,与y轴交于点C,顶点为D.