题目内容
8. 如图,在长度为1个单位长度的小正方形组成的长方形中,点A,B,C在小正方形的顶点上.
如图,在长度为1个单位长度的小正方形组成的长方形中,点A,B,C在小正方形的顶点上.(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)计算△ABC的面积;
(3)在直线l上找一点P,使PB+PC的长最短.
分析 (1)根据网格结构找出点B、C关于直线l的对称点B′、C′的位置,然后与点A顺次连接即可;
(2)利用△ABC所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解;
(3)根据轴对称确定最短路线问题,连接B′C与直线l的交点即为所求点P.
解答 解:(1)△AB′C′如图所示;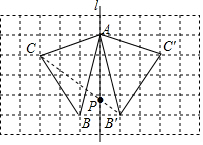
(2)△ABC的面积=3×4-$\frac{1}{2}$×2×3-$\frac{1}{2}$×1×4-$\frac{1}{2}$×1×3,
=12-3-2-1.5,
=12-6.5,
=5.5;
(3)点P如图所示.
点评 本题考查了利用轴对称确定最短路线问题,利用轴对称变换作图,熟练掌握网格结构准确找出对应点的位置是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
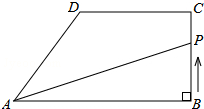 如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=8cm.BC=4cm,CD=5cm.动点P从点B开始沿折线BC-CD-DA以1cm/s的速度运动到点A.设点P运动的时间为t(s),△PAB面积为S(cm2).
如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=8cm.BC=4cm,CD=5cm.动点P从点B开始沿折线BC-CD-DA以1cm/s的速度运动到点A.设点P运动的时间为t(s),△PAB面积为S(cm2). △ABC在平面直角坐标系中的位置如图所示:
△ABC在平面直角坐标系中的位置如图所示: 如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,过D作⊙O切线DE交AC于点E.
如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,过D作⊙O切线DE交AC于点E.
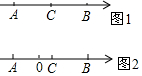 如图1,在数轴上,A点、B点与C点的距离相等.
如图1,在数轴上,A点、B点与C点的距离相等.