题目内容
11.某商场将进货单价为100元的某种商品按零售价130元一个售出时,每星期能卖出80个,商家决定降价促销,根据市场调查,每件商品每降低1元,每星期可多卖4件.(1)求商家降价前每星期的利润是多少?
(2)设每件商品降价x元,降价后每星期的利润为y元,求y与x的函数关系式.
(3)商家要使每星期的销售利润最大,应将售价定为每件多少元?每星期的最大销售利润是多少?
分析 (1)根据总利润=每个商品利润×销售量即可得;
(2)根据(1)中相等关系即可得;
(3)将(2)中函数解析式配方成顶点式即可得.
解答 解:(1)商家降价前每星期的利润是:(130-100)×80=2400元;
(2)根据题意知,y=(130-x-100)(80+4x)=-4x2+40x+2400;
(3)∵y=-4x2+40x+2400=-4(x-5)2+2500,
∴当x=5时,即售价为130-x=125元时,y取得最大值2500,
答:将售价定为每件125元,每星期的最大销售利润是2500.
点评 本题主要考查二次函数的实际应用,解题的关键是理解题意,找到题目中蕴含的相等关系列出函数解析式并配方是解题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 已知△ABN和△ACM位置如图所示,AB=AC,∠1=∠2,∠M=∠N.求证:AD=AE.
已知△ABN和△ACM位置如图所示,AB=AC,∠1=∠2,∠M=∠N.求证:AD=AE.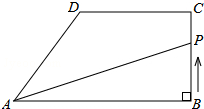 如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=8cm.BC=4cm,CD=5cm.动点P从点B开始沿折线BC-CD-DA以1cm/s的速度运动到点A.设点P运动的时间为t(s),△PAB面积为S(cm2).
如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=8cm.BC=4cm,CD=5cm.动点P从点B开始沿折线BC-CD-DA以1cm/s的速度运动到点A.设点P运动的时间为t(s),△PAB面积为S(cm2). △ABC在平面直角坐标系中的位置如图所示:
△ABC在平面直角坐标系中的位置如图所示:
 若点M为正方形ABCD边AB上任意一点,作DM=MN交∠ABC外角的平分线于点N,求∠DMN的度数.
若点M为正方形ABCD边AB上任意一点,作DM=MN交∠ABC外角的平分线于点N,求∠DMN的度数.