题目内容

15．点F为?ABCD中DC边上的点，连接AF并延长交BC的延长线于E点，并且交BD于G，求证：AG2=FG•EG．

分析 由四边形ABCD是平行四边形，可得AD∥BC，AB∥CD，即可证得△ADG∽△EBG，△ABG∽△FDG，然后由相似三角形的对应边成比例，证得结论．

解答 证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AB∥CD，
∴△ADG∽△EBG，△ABG∽△FDG，
∴AG：EG=DG：BG，FG：AG=DG：BG，
∴AG：EG=FG：AG，
∴AG2=FG•EG．

点评 此题考查了相似三角形的判定与性质以及平行四边形的性质．注意证得△ADG∽△EBG与△ABG∽△FDG是关键．

练习册系列答案
相关题目
5．计算题
（1）-8+6
（2）-20+（-5）-（-18）
（3）2-2÷$\frac{1}{5}$×5
（4）-1.25×0.4÷（-$\frac{2}{5}$）×（-8）
（5）10×（-$\frac{2}{11}$）-2×$\frac{2}{11}$+（-3）×（-$\frac{2}{11}$）
（6）-42×（$\frac{1}{6}$-$\frac{3}{14}$+$\frac{2}{7}$）．
6．把下列各数分别填入相应的集合里．
（-2）2、0、-3.14、-（-11）、$\frac{22}{7}$、-4$\frac{1}{3}$、15%、$\frac{2}{π}$、0.$\stackrel{•}{3}$、|-2$\frac{3}{5}$|，10.01001000100001…
非负整数集合：{（-2）2、0、-（-11），…}
正分数集合：{$\frac{22}{7}$、15%，0.$\stackrel{•}{3}$、|-2$\frac{3}{5}$|，  …}
无理数集合：{$\frac{2}{π}$、10.01001000100001…， …}．
3．△ABC在平面直角坐标系中的位置如图所示：
（1）画出△ABC关于x轴对称的△A1B1C1；
（2）以原点O为位似中心，在y轴左侧将△A1B1C1放大为原来的2倍，得到的△A2B2C2，请画出△A2B2C2；
（3）设P（x，y）为△ABC内任意一点，△A2B2C2内的点P′是点P经过上述两次变换后的对应点，请直接写出P′的坐标．
10．计算：
（1）|-2|-$\sqrt{9}$+（-2016）0；
（2）$\sqrt{8}$+$\sqrt{32}$-$\sqrt{2}$-$\sqrt{12}$•$\sqrt{54}$．
20．在数轴上表示下列各数：0，-|-2.5|，-（-3$\frac{1}{2}$），-2，+5，1$\frac{1}{3}$；并用“＜“连接各数．
7．分别画出如图图形的对称轴，有几条画几条．
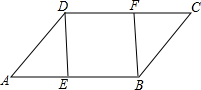4．如图，在平行四边形ABCD中，E、F分别为边AB、CD上的点，且DF=BE，连接DE、BF．求证：△ADE≌△CBF．
5．某出租车司机小李某天下午的营运全是在东西走向的人民大街上进行的，如果规定向东为正，向西为负，他这天下午行车里程（单位：千米）如下：-2，+5，-1，+10，-3，-2，+12，+4，-5，+6．
（1）将小李下午出发地记为0，他将最后一名乘客送达目的地时，小李在出发地的什么方向？距下午出发时的地点有多远？
（2）若汽车耗油量为0.08升∕千米，这天下午小李共耗油多少升？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网