��Ŀ����
��ͼ����֪������y=ax²��2ax��3(a��0)����x�ύ��A��B���㣬��y�ύ�ڵ�C����OB=3OA��
��1���������ߵĽ���ʽ��
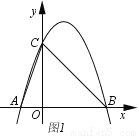
��2������BC����P����Q�ǵ�һ�����������ϲ�ͬ�����㣬�Ƿ����������P�㣬ʹ��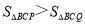 ������������ڣ�����P������꣬�������ڣ���˵�����ɣ�
������������ڣ�����P������꣬�������ڣ���˵�����ɣ�
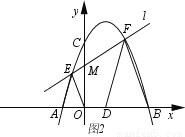
��3����ͼ2��DΪ�����ߵĶԳ�����x��Ľ��㣬MΪ�߶�OC��һ�㣬����M��ֱ��l����������E��F���㣬����AE��OE��BF��DF����AEO�ס�DFB����M������꣮
��ϰ��ϵ�д�
 ����������ϵ�д�
����������ϵ�д�
�����Ŀ
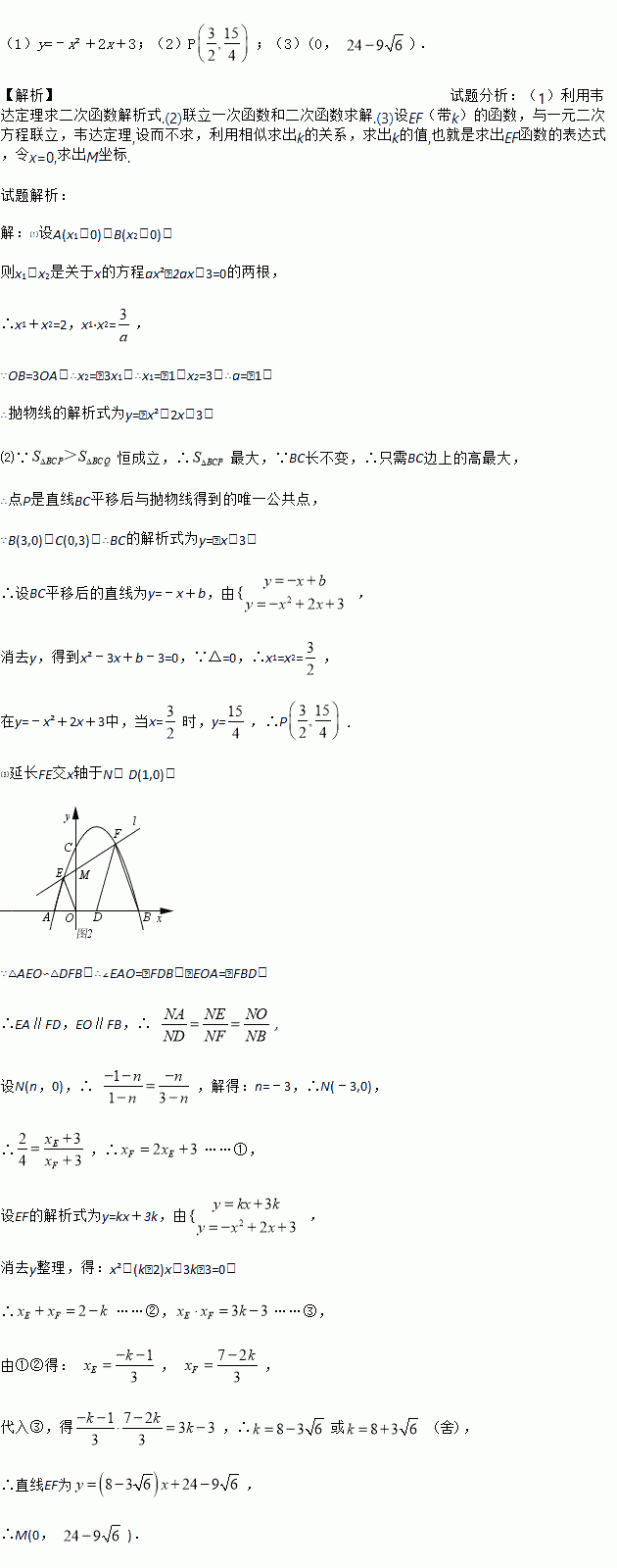

 Բ�� B.
Բ�� B.  �� C.
�� C.  Բ D.
Բ D.  ������
������
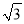 ��BC=2
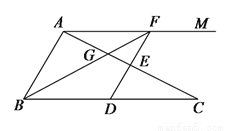
��BC=2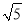 ����ͼ����Ӱ����ͼ�ε������Ϊ________��
����ͼ����Ӱ����ͼ�ε������Ϊ________�� 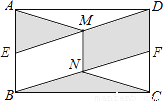
 ��
�� 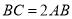 ������
������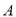 ��
��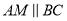 ��
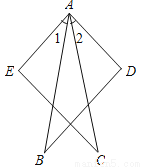
�� 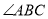 ƽ���߷ֱ�
ƽ���߷ֱ�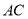 ��
�� 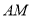 �ڵ�
�ڵ�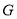 ��
�� 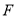 ������
������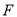 ��
��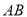 ��ƽ���ߣ��ֱ�
��ƽ���ߣ��ֱ�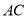 ��
�� 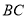 �ڵ�
�ڵ�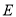 ��
�� 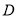 ��
��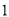 ����֤���߶�
����֤���߶�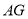 ���߶�
���߶�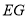 ��
��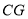 �ı������
�ı������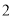 ����
����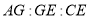 ��
��