题目内容
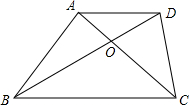如图，在梯形ABCD中，AD∥BC，对角线AC、BD相交于点O，S△OBC=p2，S△OAD=q2．求证：S四边形ABCD=（p+q）2．考点：梯形,相似三角形的判定与性质
专题：证明题
分析：设△AOB的面积为x，△DOC的面积为y，证△AOD∽△COB，求出
=
=
，推出
=
=
，
=
=
，求出x=pq，y=pq，即可得出答案．
| AO |
| OC |
| DO |
| OB |
| q |
| p |
| S△AOD |
| S△AOB |
| DO |
| OB |
| q |
| p |
| S△AOD |
| S△DOC |
| AO |
| OC |
| q |
| p |
解答：证明：设△AOB的面积为x，△DOC的面积为y，
∵AD∥BC，
∴△AOD∽△COB，
∵S△OBC=p2，S△OAD=q2，
∴
=
=
，
∴
=
=
，
=
=
，
∴x=pq，y=pq，
∴S四边形ABCD=S△AOB+S△BOC+S△DOC+S△AOD=pq+p2+pq+q2=（p+q）2．
∵AD∥BC，
∴△AOD∽△COB，
∵S△OBC=p2，S△OAD=q2，
∴
| AO |
| OC |
| DO |
| OB |
| q |
| p |
∴
| S△AOD |
| S△AOB |
| DO |
| OB |
| q |
| p |
| S△AOD |
| S△DOC |
| AO |
| OC |
| q |
| p |
∴x=pq，y=pq，
∴S四边形ABCD=S△AOB+S△BOC+S△DOC+S△AOD=pq+p2+pq+q2=（p+q）2．
点评：本题考查了相似三角形的性质和判定，三角形的面积的应用，解此题的关键是求出△ABO和△DCO的面积．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
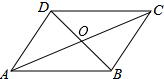如图，在四边形ABCD中，BC=12，OA=OC=13，BD=10，∠CBD=90°，求证：四边形ABCD为平行四边形．