题目内容
直线y=x-2与y轴交于点A,直线y=kx+b与y轴交于点B且与y=x-2交于点C,已知点C的纵坐标为1,且S△ABC=9,求k与b的值.
考点:两条直线相交或平行问题
专题:
分析:把C的纵坐标代入y=x-2求得横坐标,然后根据△ABC的面积=9,列出方程,求得AB的长,当B在A的上方时,B(0,4)在下方时是(0,-8).把B、C的坐标分别代入y=kx+b即可求得k、b的值;
解答:解:∵直线y=kx+b与y=x-2交于点C,点C的纵坐标为1,
∴1=x-2,解得:x=3,
∴C(3,1),
∵直线y=x-2与y轴交于点A,
∴A(0,-2),
∵S△ABC=9,
∴
AB•3=9,
∴AB=6,
∴B(0,4)或(0,-8);
把B、C的坐标分别代入y=kx+b得:
或
,
解得:
或
;
∴1=x-2,解得:x=3,
∴C(3,1),
∵直线y=x-2与y轴交于点A,
∴A(0,-2),
∵S△ABC=9,
∴
| 1 |
| 2 |
∴AB=6,
∴B(0,4)或(0,-8);
把B、C的坐标分别代入y=kx+b得:
|
|
解得:
|
|
点评:此题考查了待定系数法求一次函数的解析式、三角形面积问题、以及点与一次函数的性质.注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
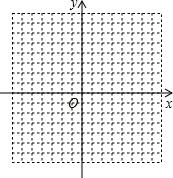 (1)在平面直角坐标系中,作出下列各点,A(-3,4),B(-3,-2),O(0,0),并把各点连起来.
(1)在平面直角坐标系中,作出下列各点,A(-3,4),B(-3,-2),O(0,0),并把各点连起来.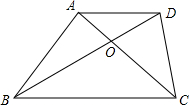 如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,S△OBC=p2,S△OAD=q2.求证:S四边形ABCD=(p+q)2.
如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,S△OBC=p2,S△OAD=q2.求证:S四边形ABCD=(p+q)2.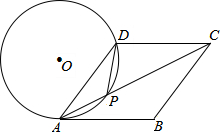 如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD
如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD