题目内容
如果将正整数M放在正整数m左侧,所得到的新数可被7整除,那么称M为m的“魔术数”(例如,把86放在415的左侧,得到的数86415能被7整除,所以称86为415的魔术数).求正整数n的最小值,使得存在互不相同的正整数a1,a2,…,an,满足对任意一个正整数m,在a1,a2,…,an中都至少有一个为m的魔术数.
考点:抽屉原理
专题:
分析:首先分n≤6和n≥7两种情况探讨,根据被7除的余数有0、1、2、3、4、5、6,利用余数差的特征分析探讨即可.
解答:解:若n≤6,取m=1,2,…,7,
根据抽屉原理知,必有a1,a2,…,an中的一个正整数M是i,
j(1≤i<j≤7)的公共的魔术数,即7|(10M+i),7|(10M+j).
则有7|(j-i),但0<j-i≤6,矛盾.
故n≥7.
又当a1,a2,…,an为1,2,…,7时,对任意一个正整数m,设其为k位数(k为正整数).
则10ki+m(i=1,2,…,7)被7除的余数两两不同.
若不然,存在正整数i,j(1≤i<j≤7),满足7|[(10kj+m)-(10ki+m)],即7|10k(j-i),从而7|(j-i),矛盾.
故必存在一个正整数i(1≤i≤7),使得7|(10ki+m),即i为m的魔术数.
故n的最小值为7.
根据抽屉原理知,必有a1,a2,…,an中的一个正整数M是i,
j(1≤i<j≤7)的公共的魔术数,即7|(10M+i),7|(10M+j).
则有7|(j-i),但0<j-i≤6,矛盾.
故n≥7.
又当a1,a2,…,an为1,2,…,7时,对任意一个正整数m,设其为k位数(k为正整数).
则10ki+m(i=1,2,…,7)被7除的余数两两不同.
若不然,存在正整数i,j(1≤i<j≤7),满足7|[(10kj+m)-(10ki+m)],即7|10k(j-i),从而7|(j-i),矛盾.
故必存在一个正整数i(1≤i≤7),使得7|(10ki+m),即i为m的魔术数.
故n的最小值为7.
点评:此题主要考查抽屉原理的实际运用,利用被一个数除的余数的特点,建立抽屉解决问题.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
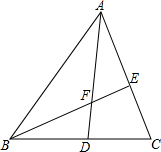 如图,在△ABC中,AD平分∠BAC交BC于D,BE⊥AC于E,交AD于F,求证:∠AFE=
如图,在△ABC中,AD平分∠BAC交BC于D,BE⊥AC于E,交AD于F,求证:∠AFE= (1)在平面直角坐标系中,作出下列各点,A(-3,4),B(-3,-2),O(0,0),并把各点连起来.
(1)在平面直角坐标系中,作出下列各点,A(-3,4),B(-3,-2),O(0,0),并把各点连起来.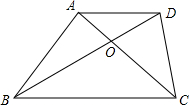 如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,S△OBC=p2,S△OAD=q2.求证:S四边形ABCD=(p+q)2.
如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,S△OBC=p2,S△OAD=q2.求证:S四边形ABCD=(p+q)2.