Question

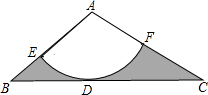如图，在△ABC上，AB=2

2

cm，AC=4cm，∠B=45°，以A为圆心的弧和BC相切于点D，分别交AB、AC于E、F两点．
（1）求

EDF

和线段BE、BC、CF所围成阴影部分的面积；
（2）若以扇形AEF围成一个圆锥，求这个圆锥的底面半径．

Answer 1

考点：切线的性质,扇形面积的计算,圆锥的计算

专题：

分析：（1）首先连接AD，由以A为圆心的弧和BC相切于点D，可得AD⊥BC，又由在△ABC上，AB=2

2

cm，AC=4cm，∠B=45°，可求得AD，BD，C的长，继而求得∠BAD与∠CAD的度数，继而求得答案；
（2）由（1）即可求得扇形AEF的弧长，继而求得答案．

解答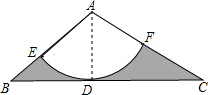：解：（1）连接AD，
∵以A为圆心的弧和BC相切于点D，
∴AD⊥BC，
∵AB=2

2

cm，∠B=45°，
∴AD=BD=2cm，∠BAD=45°，
∵AC=4cm，
∴CD=

AC2-AD2

=2

3

（cm），
∵cos∠C=

AD

AC

=

1

2

，
∴∠CAD=60°，
∴∠BAC=∠BAD+∠CAD=105°，
∴S_△ABC=S_△ABD+S_△ACD=

1

2

AD•BD+

1

2

CD•AD=

1

2

×2×2+

1

2

×2

3

×2=2+2

2

（cm²），S_扇形AEF=

105×π×22

360

=

7

6

π（cm²），
∴S_阴影=S_△ABC-S_扇形AEF=2+2

2

-

7

6

π（cm²）；

（2）∵

EDF

=

105×π×2

360

=

7

12

π（cm），
∴这个圆锥的底面半径：

7

12

π÷2π=

7

24

（cm）．

点评：此题考查了切线的性质、直角三角形的性质以及扇形的面积、弧长公式．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．