题目内容
如图，△ABC中，AB=AC，∠BAC=36°，∠ABC的平分线交AC于E点．（1）求
| BC |
| AB |
（2）求sin18°．
考点：黄金分割,解直角三角形
专题：计算题
分析：（1）利用等腰三角形的性质和角平分线的定义通过计算角度证明AE=BE=BC，再利用△ABC∽△BCE得到BC：CE=AC：BC，则AE：CE=AC：AE，于是根据黄金分割的定义得到点E为AC的黄金分割点，所以
=
，于是有
=
；
（2）作AH⊥BC于H，如图，根据等腰三角形的性质得BH=CH，∠BAH=
∠BAC=18°，在Rt△ABH中，利用正弦的定义得sin∠BAH=sin18°=
=
•
，然后利用
=
，可计算出sin18°的值．
| AE |
| AC |
| ||
| 2 |
| BC |
| AB |
| ||
| 2 |
（2）作AH⊥BC于H，如图，根据等腰三角形的性质得BH=CH，∠BAH=
| 1 |
| 2 |
| BH |
| AB |
| 1 |
| 2 |
| BC |
| AB |
| BC |
| AB |
| ||
| 2 |
解答：解：（1）∵AB=AC，∠BAC=36°，
∴∠ABC=∠C=72°，
∵BE平分∠ABC，
∴∠ABE=∠CBE=36°，
∴EA=EB，
∵∠BEC=∠A+∠ABE=72°，
∴BE=BC，
∴AE=BE=BC，
∵∠CBE=∠A=36°，∠ACB=∠BCE，
∴△ABC∽△BCE，
∴BC：CE=AC：BC，
∴AE：CE=AC：AE，
∴点E为AC的黄金分割点，
∴
=
，
∴
=
；
（2）作AH⊥BC于H，如图，
∵AB=AC，
∴BH=CH，AH平分∠BAC，
∴∠BAH=
∠BAC=18°，
在Rt△ABH中，sin∠BAH=sin18°=
=
•
，
而
=
，
∴sin18°=
•
=
．
∴∠ABC=∠C=72°，
∵BE平分∠ABC，
∴∠ABE=∠CBE=36°，
∴EA=EB，
∵∠BEC=∠A+∠ABE=72°，
∴BE=BC，
∴AE=BE=BC，
∵∠CBE=∠A=36°，∠ACB=∠BCE，
∴△ABC∽△BCE，
∴BC：CE=AC：BC，
∴AE：CE=AC：AE，
∴点E为AC的黄金分割点，
∴
| AE |
| AC |
| ||
| 2 |
∴
| BC |
| AB |
| ||
| 2 |
（2）作AH⊥BC于H，如图，
∵AB=AC，
∴BH=CH，AH平分∠BAC，
∴∠BAH=
| 1 |
| 2 |
在Rt△ABH中，sin∠BAH=sin18°=
| BH |
| AB |
| 1 |
| 2 |
| BC |
| AB |
而
| BC |
| AB |
| ||
| 2 |
∴sin18°=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
点评：本题考查了黄金分割：把线段AB分成两条线段AC和BC（AC＞BC），且使AC是AB和BC的比例中项（即AB：AC=AC：BC），叫做把线段AB黄金分割，点C叫做线段AB的黄金分割点，其中AC=
AB≈0.618AB，并且线段AB的黄金分割点有两个．也考查了正弦的定义．
| ||
| 2 |
练习册系列答案
名校课堂系列答案
相关题目
已知：如图，C是AB的中点，AE=BD，∠A=∠B．求证：∠ACE=∠BCD．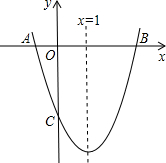
如图，已知抛物线y=ax2+bx-3的对称轴为直线x=1，交x轴于A、B两点，交y轴于C点，其中B点的坐标为（3，0）．
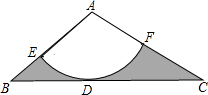如图，在△ABC上，AB=