题目内容
4.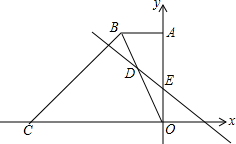 如图,直角梯形OABC的顶点C,A分别在x轴、y轴上,AB∥OC,∠AOC=90°,∠OCB=45°,BC=6$\sqrt{2}$,直线DE交OB于点D,交y轴于点E,OD=2BD,且OE,OC的长分别为方程x2-11x+18=0的两个根(OE<OC).
如图,直角梯形OABC的顶点C,A分别在x轴、y轴上,AB∥OC,∠AOC=90°,∠OCB=45°,BC=6$\sqrt{2}$,直线DE交OB于点D,交y轴于点E,OD=2BD,且OE,OC的长分别为方程x2-11x+18=0的两个根(OE<OC).(1)求出点B的坐标.
(2)求出直线DE的解析式.
(3)若点P为y轴上一点,在坐标平面内是否存在点Q,使以D,E,P,Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
分析 (1)由一元二次方程的解,确定出0E,OC,再根据勾股定理得出BG,CG,从而得出结论;
(2)由DH∥AB,得出 $\frac{OD}{OB}=\frac{DH}{AB}=\frac{OH}{OA}$,求出点D的坐标,由D,E确定出直线DE解析式;
(3)由(2)知点D,E坐标和DE解析式,再结合菱形的性质即可得出结论.
解答 (1)如图1,
∵x2-11x+18=0,
∴x=2或x=9,
∵OE<OC,
∴OE=2,OC=9,
过点B作BG⊥OC,垂足为G
∵∠OCB=45°,BC=6$\sqrt{2}$,
∴BG=CG=6,
∴OG=3,
∴B(-3,6),
(2)如图2,
过点D作DH∥AB,交y轴于点H
∴$\frac{OD}{OB}=\frac{DH}{AB}=\frac{OH}{OA}$,
∵OD=2BD,
∴DH=2,OH=4,
∴D(-2,4),
设直线DE解析式为y=kx+b,
过点D(-2,4),E(0,2),
∴DE解析式为 y=-x+2;
(3)存在Q,
如图3, 由(2)知,点D(-2,4),E(0,2),
由(2)知,点D(-2,4),E(0,2),
∴DE=2$\sqrt{2}$,
∵四边形DEPQ是菱形,
∴EP=DE=2$\sqrt{2}$,
∴P1(0,2$\sqrt{2}$+2),P2(0,2-2$\sqrt{2}$),
∵四边形DEPQ是菱形,
∴DQ∥PE,DQ=DE=2$\sqrt{2}$,
∴Q1(-2,4+2$\sqrt{2}$),Q2(-2,4-2$\sqrt{2}$),
由(2)知,直线DE的解析式为y=-x+2,
∴线段DE的垂直平分线的解析式为y=x+4,
∴P3(0,4),
∴Q3(-2,2)
∵四边形DEPQ是菱形,
∴点Q4与D关于DP4对称,
∴Q4(2,4);
综上所述,存在点Q,使以D、E、P、Q为顶点的四边形是菱形;
点Q的坐标为:Q1(-2,4+2$\sqrt{2}$),Q2(-2,4-2$\sqrt{2}$),Q3(-2,2)Q4(2,4).
点评 此题是四边形综合题,用到的知识点是一次函数的图象与性质、相似三角形的判定与性质,对称的性质,关键是根据相似求出线段的长度得出点的坐标.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案 如图是将正方体切去一个角后形成的几何体,则其主(正)视图为( )
如图是将正方体切去一个角后形成的几何体,则其主(正)视图为( )



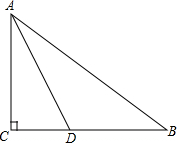 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F.
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F. 如图所示,有一根黑色金属丝镶嵌在一个完全透明的正方体表面,则该正方体的左视图是( )
如图所示,有一根黑色金属丝镶嵌在一个完全透明的正方体表面,则该正方体的左视图是( )



 如图,将三角板的直角顶点放在直尺的一边上,若∠1=68°,则∠2的度数为22°.
如图,将三角板的直角顶点放在直尺的一边上,若∠1=68°,则∠2的度数为22°. 如图,将边长为2的正方形纸片ABCD折叠,使点B落在CD上,落点记为E(不与点C,D重合),点A落在点F处,折痕MN交AD于点M,交BC于点N.
如图,将边长为2的正方形纸片ABCD折叠,使点B落在CD上,落点记为E(不与点C,D重合),点A落在点F处,折痕MN交AD于点M,交BC于点N.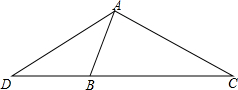 如图,在△ADC中,点B是边DC上的一点,∠DAB=∠C,$\frac{AD}{DC}$=$\frac{2}{3}$.若△ADC的面积为18cm,求△ABC的面积.
如图,在△ADC中,点B是边DC上的一点,∠DAB=∠C,$\frac{AD}{DC}$=$\frac{2}{3}$.若△ADC的面积为18cm,求△ABC的面积.