题目内容
7. 如图,PQ是⊙O的切线,Q是切点,若OQ=5,OP=9,则∠P的度数是34°(结果精确到1°).
如图,PQ是⊙O的切线,Q是切点,若OQ=5,OP=9,则∠P的度数是34°(结果精确到1°).
分析 由切线的性质得出PQ⊥OQ,由三角函数即可得出答案.
解答 解:∵PQ是⊙O的切线,Q是切点,
∴PQ⊥OQ,
∴sinP=$\frac{OQ}{OP}$=$\frac{5}{9}$≈0.5556,
∴∠P≈34°;
故答案为:34°
点评 本题考查了切线的性质以及三角函数;熟练掌握切线的性质,求出∠P的正弦值是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.下列各组角中,∠1与∠2是对顶角的为( )
| A. |  | B. |  | C. |  | D. |  |
1.某市为美化城市,有关部门决定利用现有的4200盆甲种花卉和3090盆乙种花卉,搭配成A、B两种园艺造型共60个,摆放于主干街道的两侧,搭配每个造型所需花卉数量的情况如下表所示,结合上述信息,解答下列问题:
(1)符合题意的搭配方案有几种?
(2)如果搭配一个A种造型的成本为600元,搭配一个B种造型的成本为800元,试说明选用那种方案成本最低?最低成本为多少元?
| 造型花卉 | 甲 | 乙 |
| A | 80 | 40 |
| B | 50 | 70 |
(2)如果搭配一个A种造型的成本为600元,搭配一个B种造型的成本为800元,试说明选用那种方案成本最低?最低成本为多少元?
 如图,在△ABC中,∠A=50°,∠B=70°,点D在BC的延长线上,那么∠ACD=120°.
如图,在△ABC中,∠A=50°,∠B=70°,点D在BC的延长线上,那么∠ACD=120°.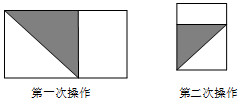 将长为1,宽为a的长方形纸片$({\frac{1}{2}<a<1})$如图那样折一下,剪下一个边长等于长方形的宽度的正方形(称为第一次操作);再把剩下的长方形如图那样折一下,剪下一个边长等于此时长方形宽度的正方形(称为第二次操作);如些反复操作下去,若在第n次操作后剩下的长方形为正方形,则操作终止.
将长为1,宽为a的长方形纸片$({\frac{1}{2}<a<1})$如图那样折一下,剪下一个边长等于长方形的宽度的正方形(称为第一次操作);再把剩下的长方形如图那样折一下,剪下一个边长等于此时长方形宽度的正方形(称为第二次操作);如些反复操作下去,若在第n次操作后剩下的长方形为正方形,则操作终止.