题目内容
16. 某菜农搭建了一个横截面为抛物线的大棚,尺寸如图:
某菜农搭建了一个横截面为抛物线的大棚,尺寸如图:(1)如图建立平面直角坐标系,使抛物线对称轴为y轴,求该抛物线的解析式;
(2)若需要开一个截面为矩形的门(如图所示),已知门的高度为1.60米,那么门的宽度最大是多少米(不考虑材料厚度)?(结果保留根号)
分析 (1)根据题意设出二次函数的解析式,把图象上点的坐标代入即可求出二次函数的解析式;
(2)令y=1.6,求出x的值,即可确定门的最大宽度.
解答 解:(1)由图可设抛物线的解析式为:y=ax2+2,
由图知抛物线与x轴正半轴的交点为(2,0),则:a×22+2=0,
∴a=-$\frac{1}{2}$,
∴抛物线的解析式为y=-$\frac{1}{2}$x2+2;
(2)当y=1.60时,知1.6=-$\frac{1}{2}$x2+2,
解得:x=$±\frac{2\sqrt{5}}{5}$,
所以门的宽度最大为2×$\frac{2\sqrt{5}}{5}$=$\frac{4\sqrt{5}}{5}$米.
点评 本题主要考查二次函数的实际应用能力,能根据题意设出合适的函数表达式是关键.

练习册系列答案
相关题目
17.△ABC是⊙O的内接三角形,⊙O的直径为10,∠ABC=60°,则AC的长是( )
| A. | 5 | B. | 10 | C. | 5$\sqrt{2}$ | D. | 5$\sqrt{3}$ |
 用6m长的铝合金型材做一个形状如图所示的矩形窗框,若窗框的面积为1.5m2(铝合金型材宽度不计),求该窗框的长和宽各为多少?
用6m长的铝合金型材做一个形状如图所示的矩形窗框,若窗框的面积为1.5m2(铝合金型材宽度不计),求该窗框的长和宽各为多少? 如图,已知△ABD是一张直角三角形纸片,其中∠A=90°,∠ADB=30°,小亮将它绕点A逆时针旋转β(0<β<180°)后得到△AMF,AM交直线BD于点K.
如图,已知△ABD是一张直角三角形纸片,其中∠A=90°,∠ADB=30°,小亮将它绕点A逆时针旋转β(0<β<180°)后得到△AMF,AM交直线BD于点K. 如图,直线AB,CD相交于点O,OE平分∠AOD,OF⊥OC,
如图,直线AB,CD相交于点O,OE平分∠AOD,OF⊥OC,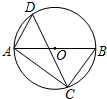 如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=54°,则∠BAC=36°.
如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=54°,则∠BAC=36°.