题目内容
如图①所示,已知A(2
,
),O(0,0),C(5
,
),B(3
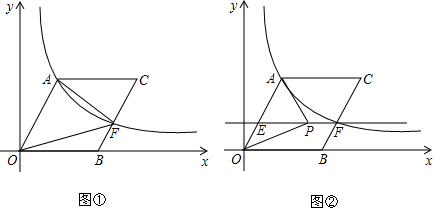
,0),连接AO、OB、BC、CA,构成四边形AOBC为平行四边形,F为BC中点,过点F作EF∥OB,交OA于点E(如图②),点P为直线EF上的一个动点,连接PA、PO.是否存在这样的点P,使以P、O、A为顶点的三角形是直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
| 3 |
8
| ||
| 3 |
| 3 |
8
| ||
| 3 |
| 3 |

考点:反比例函数综合题,直角三角形斜边上的中线,勾股定理,平行线分线段成比例,相似三角形的判定与性质
专题:分类讨论
分析:由于Rt△OPA的直角不确定,因此需分三种情况(①∠OPA=90°,②∠OAP=90°,③∠POA=90°)讨论.运用勾股定理可求出AH、OH、OA,然后根据平行线等分线段定理可得OE=AE,OG=GH,从而可求出OG、OE、EG,然后运用相似三角形的性质及直角三角形斜边上的中线等于斜边的一半等知识,就可解决问题.
解答:解:存在点P,使以P、O、A为顶点的三角形是直角三角形,
点P的坐标为(
,
)、(-
,
)、(
,
)、(-
,
).
理由如下:
设直线EF与y轴的交点为G,延长CA交y轴于点H,
∵四边形AOBC是平行四边形,∴AC∥OB.
∵OB⊥OH,∴AC⊥OH.
∵点A的坐标为(2
,
),
∴AH=2
,OH=
,
∴OA=
=
.
∵GF∥OB,CH∥OB,∴OB∥GF∥CH.
∵BF=CF,
∴OE=AE=
OA=
,OG=GH=
OH=
.
∴EG=
=
.
①若∠OPA=90°,
Ⅰ.点P在点E的右边,如图②.

∵∠OPA=90°,OE=AE,
∴PE=
OA=
.
∴PG=PE+EG=
+
=
.
∴点P的坐标为(
,
).
Ⅱ.点P在点E的左边,如图③.

∵∠OPA=90°,OE=AE,
∴PE=
OA=
.
∴PG=PE-EG=
-
=
.
∴点P的坐标为(-
,
).
②若∠OAP=90°,如图④.

∵∠OGE=∠PAE,∠GEO=∠AEP,
∴△OGE∽△PAE.
∴
=
.
∴OE•AE=GE•PE.
∴
×
=
PE.
∴PE=
.
∴GP=GE+PE=
+
=
.
∴点P的坐标为(
,
).
③若∠POA=90°,如图⑤.

∵∠POE=∠OGE=90°,∠PEO=∠OEG,
∴△POE∽△OGE.
∴
=
.
∴OE•OE=GE•PE.
∴
×
=
PE.
∴PE=
.
∴PG=PE-EG=
-
=
.
∴点P的坐标为(-
,
).
综上所述:满足要求的点P的坐标为(
,
)、(-
,
)、(
,
)、(-
,
).
点P的坐标为(
8
| ||
| 3 |
4
| ||
| 3 |
2
| ||
| 3 |
4
| ||
| 3 |
34
| ||
| 9 |
4
| ||
| 3 |
16
| ||
| 9 |
4
| ||
| 3 |
理由如下:
设直线EF与y轴的交点为G,延长CA交y轴于点H,
∵四边形AOBC是平行四边形,∴AC∥OB.
∵OB⊥OH,∴AC⊥OH.
∵点A的坐标为(2
| 3 |
8
| ||
| 3 |
∴AH=2
| 3 |
8
| ||
| 3 |
∴OA=
| AH2+OH2 |
10
| ||
| 3 |
∵GF∥OB,CH∥OB,∴OB∥GF∥CH.
∵BF=CF,
∴OE=AE=
| 1 |
| 2 |
5
| ||
| 3 |
| 1 |
| 2 |
4
| ||
| 3 |
∴EG=
| OE2-OG2 |
| 3 |
①若∠OPA=90°,
Ⅰ.点P在点E的右边,如图②.

∵∠OPA=90°,OE=AE,
∴PE=
| 1 |
| 2 |
5
| ||
| 3 |
∴PG=PE+EG=
5
| ||
| 3 |
| 3 |
8
| ||
| 3 |
∴点P的坐标为(
8
| ||
| 3 |
4
| ||
| 3 |
Ⅱ.点P在点E的左边,如图③.

∵∠OPA=90°,OE=AE,
∴PE=
| 1 |
| 2 |
5
| ||
| 3 |
∴PG=PE-EG=
5
| ||
| 3 |
| 3 |
2
| ||
| 3 |
∴点P的坐标为(-
2
| ||
| 3 |
4
| ||
| 3 |
②若∠OAP=90°,如图④.

∵∠OGE=∠PAE,∠GEO=∠AEP,
∴△OGE∽△PAE.
∴
| OE |
| PE |
| GE |
| AE |
∴OE•AE=GE•PE.
∴
5
| ||
| 3 |
5
| ||
| 3 |
| 3 |
∴PE=
25
| ||
| 9 |
∴GP=GE+PE=
| 3 |
25
| ||
| 9 |
34
| ||
| 9 |
∴点P的坐标为(
34
| ||
| 9 |
4
| ||
| 3 |
③若∠POA=90°,如图⑤.

∵∠POE=∠OGE=90°,∠PEO=∠OEG,
∴△POE∽△OGE.
∴
| OE |
| GE |
| PE |
| OE |
∴OE•OE=GE•PE.
∴
5
| ||
| 3 |
5
| ||
| 3 |
| 3 |
∴PE=
25
| ||
| 9 |
∴PG=PE-EG=
25
| ||
| 9 |
| 3 |
16
| ||
| 9 |
∴点P的坐标为(-
16
| ||
| 9 |
4
| ||
| 3 |
综上所述:满足要求的点P的坐标为(
8
| ||
| 3 |
4
| ||
| 3 |
2
| ||
| 3 |
4
| ||
| 3 |
34
| ||
| 9 |
4
| ||
| 3 |
16
| ||
| 9 |
4
| ||
| 3 |
点评:本题主要考查了相似三角形的判定与性质、平行线等分线段定理、勾股定理、直角三角形斜边上的中线等于斜边的一半等知识,考查了分类讨论的数学思想,运用相似三角形的性质及直角三角形斜边上的中线等于斜边的一半等知识是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列说法正确的是( )
| A、一个有理数不是正数就是负数 |
| B、一个有理数不是整数就是分数 |
| C、有理数是自然数和负整数 |
| D、有理数分为整数、分数、正数、负数、0五类 |