题目内容
3. 如图,点A、F、C、D在同一条直线上,点B,E分别在直线AD的两侧,AB∥DE,且AB=DE,∠A=∠D,AF=DC.
如图,点A、F、C、D在同一条直线上,点B,E分别在直线AD的两侧,AB∥DE,且AB=DE,∠A=∠D,AF=DC.求证:四边形BFEC是平行四边形.
分析 首先证明△AFB≌△DCE(SAS),进而得出FB=CE,FB∥CE,进而得出答案.
解答 证明:在△AFB和△DCE中,
$\left\{\begin{array}{l}{AB=DE}\\{∠A=∠D}\\{AF=DC}\end{array}\right.$,
∴△AFB≌△DCE(SAS),
∴FB=CE,
∴∠AFB=∠DCE,
∴FB∥CE,
∴四边形BFEC是平行四边形.
点评 此题主要考查了平行四边形的判定以及全等三角形的判定与性质,得出△AFB≌△DCE是解题关键.

练习册系列答案
相关题目
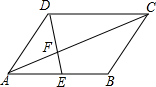 如图,?ABCD中,AE:EB=2:3,DE交AC于F.
如图,?ABCD中,AE:EB=2:3,DE交AC于F. 如图,D是△ABC的边AB上一点,CE∥AB,DE交AC于点F,若FA=FC.
如图,D是△ABC的边AB上一点,CE∥AB,DE交AC于点F,若FA=FC.
 如图,将正方形纸片按如图折叠,AM为折痕,点B落在对角线AC上的点E处,则∠CME=45°.
如图,将正方形纸片按如图折叠,AM为折痕,点B落在对角线AC上的点E处,则∠CME=45°. 如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于D点.若CD=3cm,则点D到斜边AB的距离是3cm.
如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于D点.若CD=3cm,则点D到斜边AB的距离是3cm.