题目内容
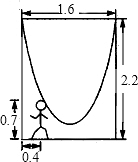 如图,一单杠高2.2米,两立柱之间的距离为1.6米,将一根绳子的两端拴于立柱与铁结合处,绳子自然下垂呈抛物线状态,一身高0.7米的小女孩站在离立柱0.4米处,其头刚好触上绳子,则绳子最低点到地面的距离为( )米.
如图,一单杠高2.2米,两立柱之间的距离为1.6米,将一根绳子的两端拴于立柱与铁结合处,绳子自然下垂呈抛物线状态,一身高0.7米的小女孩站在离立柱0.4米处,其头刚好触上绳子,则绳子最低点到地面的距离为( )米.| A、0.16 | B、0.2 |
| C、0.4 | D、0.64 |
考点:二次函数的应用
专题:
分析:要想求绳子的最低点,由题知挂在单杠上的绳子可看成抛物线,所以即使求抛物线的最低点离地面的距离,以O点为原点水平线为x轴建立坐标系,如解题部分,所以设抛物线的解析式为:y=ax2,由建立的坐标可求得A、B、D点的横坐分别为-0.8,0.8,-0.4,yA-yD=1.5,由此可求的抛物线的解析式,由D点的纵坐标与人身高的差就是所求.
解答:
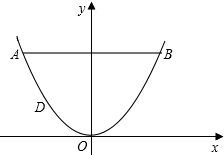 解:如图所示,以O为坐标原点,水平方向为x轴,垂直方向为y轴,建立直角坐标系,
解:如图所示,以O为坐标原点,水平方向为x轴,垂直方向为y轴,建立直角坐标系,
设抛物线的解析式为y=ax2(a≠0).
设A、B、D三点坐标依次为(xA,yA),(xB,yB),(xD,yD),由题意,得AB=1.6,
∴xA=-0.8,xB=0.8,又可得xD=-(
×1.6-0.4)=-0.4.
∴当x=-0.8时,yA=a•(-0.8)2=0.64a;
当x=-0.4时,yD=a•(-0.4)2=0.16a,
∵yA-yD=2.2-0.7=1.5,
∴0.64a-0.16a=1.5,
∴a=
,
∴抛物线解析式为y=
x2.
当x=-0.4时,yD=
×(-0.4)2=0.5,
∴0.7-0.5=0.2m.
故选B.
 解:如图所示,以O为坐标原点,水平方向为x轴,垂直方向为y轴,建立直角坐标系,
解:如图所示,以O为坐标原点,水平方向为x轴,垂直方向为y轴,建立直角坐标系,设抛物线的解析式为y=ax2(a≠0).
设A、B、D三点坐标依次为(xA,yA),(xB,yB),(xD,yD),由题意,得AB=1.6,
∴xA=-0.8,xB=0.8,又可得xD=-(
| 1 |
| 2 |
∴当x=-0.8时,yA=a•(-0.8)2=0.64a;
当x=-0.4时,yD=a•(-0.4)2=0.16a,
∵yA-yD=2.2-0.7=1.5,
∴0.64a-0.16a=1.5,
∴a=
| 25 |
| 8 |
∴抛物线解析式为y=
| 25 |
| 8 |
当x=-0.4时,yD=
| 25 |
| 8 |
∴0.7-0.5=0.2m.
故选B.
点评:本题考查的是二次函数在实际生活中的应用,正确的理解题意,找准对应量,建立正确的坐标轴,一般以尽可能的点在特殊位置为标准建坐标系,题目难度中等,注意数形结合.

练习册系列答案
相关题目
下列各数中是无理数的是( )
| A、-1 | ||
| B、3.141 | ||
C、
| ||
D、
|
直线l的解析式是y=mx+1,其中m是不等式组
的解,则直线l的图象不经过( )
|
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 已知点P在△AOB内,点M,N分别是点P关于射线OA,OB的对称点,点M,N的连线与OA,OB交于点E、F,若MN的长为20cm,求△PEF的周长.
已知点P在△AOB内,点M,N分别是点P关于射线OA,OB的对称点,点M,N的连线与OA,OB交于点E、F,若MN的长为20cm,求△PEF的周长.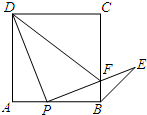 如图,正方形ABCD的边AB上有一点P(不与A、B重合),连接PD并将线段PD绕着点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE、DF.则∠CBE的度数是
如图,正方形ABCD的边AB上有一点P(不与A、B重合),连接PD并将线段PD绕着点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE、DF.则∠CBE的度数是
 已知等边三角形ABC,D为BC上一点,DE,DF垂直AB,AC,DE=2,DF=1,EF延长线交BC延长线于G,求CG的长?
已知等边三角形ABC,D为BC上一点,DE,DF垂直AB,AC,DE=2,DF=1,EF延长线交BC延长线于G,求CG的长? 如图,已知向量
如图,已知向量