题目内容
已知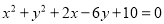 ,则
,则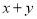 的值?
的值?
 2
【解析】试题分析:根据拆分法,构成完全平方公式,然后分解因式为非负数的和的形式,然后求解即可.
试题解析:因为,所以根据平方的非负性可以得到x=-1,y=3,则.
2
【解析】试题分析:根据拆分法,构成完全平方公式,然后分解因式为非负数的和的形式,然后求解即可.
试题解析:因为,所以根据平方的非负性可以得到x=-1,y=3,则.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法正确的是( )
A. 平移改变图形的形状
B. 平移改变图形的大小
C. 平移改变物体的形状和大小
D. 平移不改变物体的形状和大小
 D
【解析】试题解析:平移的特点是不变形,即平移不改变物体的形状和大小.
故选D.
D
【解析】试题解析:平移的特点是不变形,即平移不改变物体的形状和大小.
故选D. 用反证法证明“三角形中至少有一个内角不小于60°”,应先假设这个三角形中( )
A. 有一个内角小于60° B. 每一个内角都小于60°
C. 有一个内角大于60° D. 每一个内角都大于60°
 B
【解析】试题分析:此题要运用反证法,由题意先假设三角形的三个角都小于60°成立.然后推出不成立.得出选项.
【解析】
设三角形的三个角分别为:a,b,c.
假设,a<60°,b<60°,c<60°,
则a+b+c<60°+60°+60°,
即,a+b+c<180°与三角形内角和定理a+b+c=180°矛盾.
所以假设不成立,即三角形中至少有一个角不小于60...
B
【解析】试题分析:此题要运用反证法,由题意先假设三角形的三个角都小于60°成立.然后推出不成立.得出选项.
【解析】
设三角形的三个角分别为:a,b,c.
假设,a<60°,b<60°,c<60°,
则a+b+c<60°+60°+60°,
即,a+b+c<180°与三角形内角和定理a+b+c=180°矛盾.
所以假设不成立,即三角形中至少有一个角不小于60... 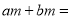 m(_________)
m(_________)
 【解析】根据提公因式法因式分解,提取公因式m可得m(a+b).
故答案为:a+b.
【解析】根据提公因式法因式分解,提取公因式m可得m(a+b).
故答案为:a+b. 一个多项式分解因式的结果是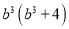 ,那么这个多项式是( )
,那么这个多项式是( )
A. 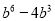 B.
B. 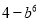 C.
C. 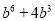 D.
D. 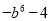
 C
【解析】利用因式分解是整式乘法的逆运算,可知=.
故选:C.
C
【解析】利用因式分解是整式乘法的逆运算,可知=.
故选:C. 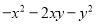 =__________
=__________
 【解析】根据因式分解的方法,先提公因式“﹣”,再根据完全平方公式分解因式为: .
故答案为: .
【解析】根据因式分解的方法,先提公因式“﹣”,再根据完全平方公式分解因式为: .
故答案为: . 将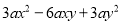 分解因式是___________
分解因式是___________
 【解析】根据题意,先提公因式,再根据平方差公式分解即可得: .
故答案为: .
【解析】根据题意,先提公因式,再根据平方差公式分解即可得: .
故答案为: . 已知:如图,点C为AB中点,CD=BE,CD∥BE.求证:△ACD≌△CBE.
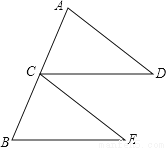
 证明见解析.
【解析】试题分析:根据中点定义求出AC=CB,根据两直线平行,同位角相等,求出∠ACD=∠B,然后利用SAS即可证明△ACD≌△CBE.
试题解析:证明:∵CD∥BE,∴∠ACD=∠B..
∵点C为AB中点,∴AC=CB.
又∵CD=BE,∴△ACD≌△CBE(SAS)
证明见解析.
【解析】试题分析:根据中点定义求出AC=CB,根据两直线平行,同位角相等,求出∠ACD=∠B,然后利用SAS即可证明△ACD≌△CBE.
试题解析:证明:∵CD∥BE,∴∠ACD=∠B..
∵点C为AB中点,∴AC=CB.
又∵CD=BE,∴△ACD≌△CBE(SAS) 某商贩去菜摊买西红柿,他上午买了30斤,价格为每斤x元;下午,他又买了20斤,价格为每斤y元,后来他以每斤 元的价格卖完后.发现自己赔了钱,你知道是什么原因吗?
元的价格卖完后.发现自己赔了钱,你知道是什么原因吗?
 见解析
【解析】试题分析:题目中的不等关系是:买黄瓜每斤平均价>卖黄瓜每斤平均价,据此列不等式进行求解即可.
试题解析:根据题意得,他买西红柿每斤平均价是元,
以每斤元的价格卖完后,结果发现自己赔了钱,
则>
解之得,x>y,
所以赔钱的原因是x>y.
即此商贩上午所买的西红柿的单价高于下午的单价,所以赔了钱.
见解析
【解析】试题分析:题目中的不等关系是:买黄瓜每斤平均价>卖黄瓜每斤平均价,据此列不等式进行求解即可.
试题解析:根据题意得,他买西红柿每斤平均价是元,
以每斤元的价格卖完后,结果发现自己赔了钱,
则>
解之得,x>y,
所以赔钱的原因是x>y.
即此商贩上午所买的西红柿的单价高于下午的单价,所以赔了钱. 
