题目内容
把多项式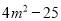 分解因式正确的是( )
分解因式正确的是( )
A. 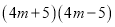 B.
B. 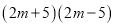
C. 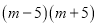 D.
D. 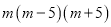
 B
【解析】利用公式法分解因式的要点,根据平方差公式: ,分解因式为: .
故选:B.
B
【解析】利用公式法分解因式的要点,根据平方差公式: ,分解因式为: .
故选:B.
练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
下列说法正确的有( )
①4是x﹣3>1的解;②不等式x﹣2<0的解有无数个;③x>5是不等式x+2>3的解集;④x=3是不等式x+2>1的解;⑤不等式x+2<5有无数个正整数解.
A.1个 B.2个 C.3个 D.4个
 B.
【解析】
试题分析:解x﹣3>1得:x>4,所以4不是x﹣3>1的解,故①错误;不等式x﹣2<0的解有无数个,此说法正确,故②正确;解不等式x+2>3得:x>1,所以x>5不是不等式x+2>3的解集,故③错误;解不等式x+2>1得:x>-1,所以x=3是不等式x+2>1的解,故④正确;解不等式x+2<5得:x<3,所以其正整数解为1,2共2个.故⑤错误.
故选B.
B.
【解析】
试题分析:解x﹣3>1得:x>4,所以4不是x﹣3>1的解,故①错误;不等式x﹣2<0的解有无数个,此说法正确,故②正确;解不等式x+2>3得:x>1,所以x>5不是不等式x+2>3的解集,故③错误;解不等式x+2>1得:x>-1,所以x=3是不等式x+2>1的解,故④正确;解不等式x+2<5得:x<3,所以其正整数解为1,2共2个.故⑤错误.
故选B. 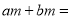 m(_________)
m(_________)
 【解析】根据提公因式法因式分解,提取公因式m可得m(a+b).
故答案为:a+b.
【解析】根据提公因式法因式分解,提取公因式m可得m(a+b).
故答案为:a+b. 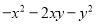 =__________
=__________
 【解析】根据因式分解的方法,先提公因式“﹣”,再根据完全平方公式分解因式为: .
故答案为: .
【解析】根据因式分解的方法,先提公因式“﹣”,再根据完全平方公式分解因式为: .
故答案为: . 将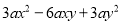 分解因式是___________
分解因式是___________
 【解析】根据题意,先提公因式,再根据平方差公式分解即可得: .
故答案为: .
【解析】根据题意,先提公因式,再根据平方差公式分解即可得: .
故答案为: . 下列多项式中,能用公式法分解因式的是( )
A. m2-mn B. m2+mn C. m2-n2 D. m2+n2
 C
【解析】根据平方差公式的特点: ,可知C符合题意.
故选:C.
C
【解析】根据平方差公式的特点: ,可知C符合题意.
故选:C. 已知:如图,点C为AB中点,CD=BE,CD∥BE.求证:△ACD≌△CBE.
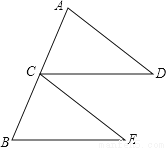
 证明见解析.
【解析】试题分析:根据中点定义求出AC=CB,根据两直线平行,同位角相等,求出∠ACD=∠B,然后利用SAS即可证明△ACD≌△CBE.
试题解析:证明:∵CD∥BE,∴∠ACD=∠B..
∵点C为AB中点,∴AC=CB.
又∵CD=BE,∴△ACD≌△CBE(SAS)
证明见解析.
【解析】试题分析:根据中点定义求出AC=CB,根据两直线平行,同位角相等,求出∠ACD=∠B,然后利用SAS即可证明△ACD≌△CBE.
试题解析:证明:∵CD∥BE,∴∠ACD=∠B..
∵点C为AB中点,∴AC=CB.
又∵CD=BE,∴△ACD≌△CBE(SAS) 如图,已知E,F是AC上的两点,AE=CF,DF=BE,∠AFD=∠CEB,则下列不成立的是( )
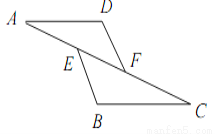
A. ∠A=∠C B. AD=CB C. BC=DF D. DF∥BE
 C
【解析】∵AE=CF(已知),
∴AE+EF=EF+CF,
∴AF=EC,
∵∠AFD=∠CEB,
∴△AFD≌△CEB(SAS),
∴∠A=∠C,
AD=CB,BC=DA,
∵∠AFD=∠CEB,
∴DF∥BE.
故选:C.
C
【解析】∵AE=CF(已知),
∴AE+EF=EF+CF,
∴AF=EC,
∵∠AFD=∠CEB,
∴△AFD≌△CEB(SAS),
∴∠A=∠C,
AD=CB,BC=DA,
∵∠AFD=∠CEB,
∴DF∥BE.
故选:C. 一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A.7 B.7或8 C.8或9 D.7或8或9
 D.
【解析】
试题分析:设内角和为1080°的多边形的边数是n,则(n﹣2)•180°=1080°,解得:n=8.
则原多边形的边数为7或8或9.故选D.
D.
【解析】
试题分析:设内角和为1080°的多边形的边数是n,则(n﹣2)•180°=1080°,解得:n=8.
则原多边形的边数为7或8或9.故选D. 
