题目内容
12.(1)解不等式组$\left\{\begin{array}{l}x+2≥1\\ 2(x+3)-3>3x\end{array}\right.$(2)化简:1-$\frac{a-2}{a}$÷$\frac{{a}^{2}-4}{{a}^{2}+a}$.
分析 (1)根据解不等式组的方法可以求得原不等式组的解集;
(2)根据分式的除法和减法可以解答本题.
解答 解:(1)$\left\{\begin{array}{l}{x+2≥1}&{①}\\{2(x+3)-3>3x}&{②}\end{array}\right.$
由①,得x≥-1,
由②,得x<3,
∴原不等式组的解集是-1≤x<3;
(2)1-$\frac{a-2}{a}$÷$\frac{{a}^{2}-4}{{a}^{2}+a}$
=1-$\frac{a-2}{a}×\frac{a(a+1)}{(a+2)(a-2)}$
=1-$\frac{a+1}{a+2}$
=$\frac{a+2-a-1}{a+2}$
=$\frac{1}{a+2}$.
点评 本题考查分式的混合运算、解一元一次不等式组,解题的关键是明确分式的混合运算的计算方法和解一元一次不等式组的方法.

练习册系列答案
相关题目
4. 了了解九年级男生的立定跳远成绩,体育老师对该校九年级的260位男生进行了一次立定跳远测试.已知,九年级男生立定跳远成绩(x)的达标要求是:x<185为不合格;185≤x<225为合格;x≥225为优秀(单位:cm).随机以40位男为生的测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下所示:
了了解九年级男生的立定跳远成绩,体育老师对该校九年级的260位男生进行了一次立定跳远测试.已知,九年级男生立定跳远成绩(x)的达标要求是:x<185为不合格;185≤x<225为合格;x≥225为优秀(单位:cm).随机以40位男为生的测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下所示:
请结合图表完成下列问题:
(1)请把频数分布表和频数分布直方图补充完整;
(2)这个样本数据的中位数落在第几组?
(3)估计该校九年级男生立定跳远成绩为优秀的有多少人?
 了了解九年级男生的立定跳远成绩,体育老师对该校九年级的260位男生进行了一次立定跳远测试.已知,九年级男生立定跳远成绩(x)的达标要求是:x<185为不合格;185≤x<225为合格;x≥225为优秀(单位:cm).随机以40位男为生的测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下所示:
了了解九年级男生的立定跳远成绩,体育老师对该校九年级的260位男生进行了一次立定跳远测试.已知,九年级男生立定跳远成绩(x)的达标要求是:x<185为不合格;185≤x<225为合格;x≥225为优秀(单位:cm).随机以40位男为生的测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下所示:| 组别 | 成绩x(cm) | 频数(人数) |
| 第1组 | 165≤x<185 | 4 |
| 第2组 | 185≤x<205 | 6 |
| 第3组 | 205≤x<225 | |
| 第4组 | 225≤x<245 | 18 |
| 第5组 | 245≤x<265 | 4 |
(1)请把频数分布表和频数分布直方图补充完整;
(2)这个样本数据的中位数落在第几组?
(3)估计该校九年级男生立定跳远成绩为优秀的有多少人?
 某数学兴趣小组在全校范围内,对四种沙县小吃:馄饨、拌面、烧麦、芋饺进行“我最喜爱的沙县小吃”调查活动,并随即抽取了50名同学的调查问卷,整理后绘制成如图所示的条形统计图,请根据所给信息解答以下问题:
某数学兴趣小组在全校范围内,对四种沙县小吃:馄饨、拌面、烧麦、芋饺进行“我最喜爱的沙县小吃”调查活动,并随即抽取了50名同学的调查问卷,整理后绘制成如图所示的条形统计图,请根据所给信息解答以下问题: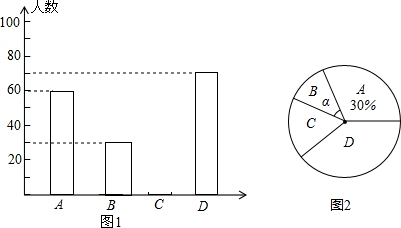 黔东南州某中学为了解本校学生平均每天的课外学习实践情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学生时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题:
黔东南州某中学为了解本校学生平均每天的课外学习实践情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学生时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题: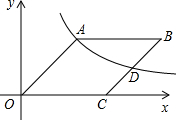 如图,O为坐标原点,点C在x轴的正半轴上,四边形OABC是平行四边形,∠AOC=45°,OA=2,反比例函数y=$\frac{k}{x}$在第一现象内的图象经过点A,与BC交于点D.
如图,O为坐标原点,点C在x轴的正半轴上,四边形OABC是平行四边形,∠AOC=45°,OA=2,反比例函数y=$\frac{k}{x}$在第一现象内的图象经过点A,与BC交于点D.