题目内容
7．
如图，AD是△ABC的中线，∠ADC=45°．把△ADC沿直线AD折过来，点C落在点C′的位置上，如果BC=2，那么BC′=$\sqrt{2}$．
分析 首先根据折叠的性质可得：∠ADC=∠ADC′=45°，即DC′⊥DC，且DC=DC′=BD，由此可得△BDC′是个直角边为4的等腰直角三角形，由此得解．
解答 解：∵把△ABC沿直线AD折过来，点C落在点C′的位置，
∴△ADC≌△ADC′，
∴∠ADC=∠ADC′=45°，DC=DC′=BD，
∴△BDC′是等腰直角三角形，且直角边为1，
那么斜边BC′=$\sqrt{2}$．
故答案为：$\sqrt{2}$．
点评 此题主要考查的是图形的翻折变换，能够判断出△BDC′的形状是解答此题的关键．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
13．
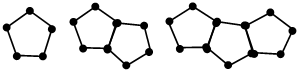用火柴棒按如图的方式搭五边形组成的图形
（1）填写表：
（2）照这样的规律搭下去，搭n个这样的五边形需要（4n+1）根火柴棒．
用火柴棒按如图的方式搭五边形组成的图形（1）填写表：
| 五边形个数 | 1 | 2 | 3 | 4 | 5 |
| 火柴棒根数 | 5 | 9 | 13 | 17 |
如图所示，在△ABC中，点E是BC上一点，BE=2CE，点F是AE的中点，那么AD：DC=$\frac{2}{3}$，BF：FD=4．