Question

16．如图所示，在△ABC中，点E是BC上一点，BE=2CE，点F是AE的中点，那么AD：DC=$\frac{2}{3}$，BF：FD=4．

Answer 1

分析 作EH∥BD交AC于H，作FG∥AC交BC于G，根据平行线分线段成比例定理解答即可．

解答 解：如图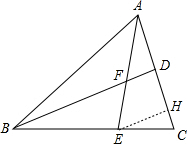，作EH∥BD交AC于H，
则$\frac{CH}{HD}$=$\frac{CE}{EB}$=$\frac{1}{2}$，DH=DA，
∴AD：DC=$\frac{2}{3}$；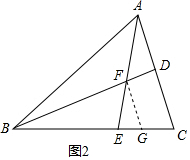
如图2，作FG∥AC交BC于G，
则EG=GC，又BE=2CE，
∴BF：FD=BG：GC=4，
故答案为：$\frac{2}{3}$；4．

点评 本题考查的是平行线分线段成比例定理，灵活运用定理、正确作出辅助线、找准对应关系是解题的关键．