题目内容
解方程:
(1)4(x-2)-[5(1-2x)-4(5x-1)]=0;
(2)
-
=
-1
(3)
[2(x-
)+
]=5x
(4)
(5x+1)=
(9x+1)-
(1-x)
(5)
=
+
.
(1)4(x-2)-[5(1-2x)-4(5x-1)]=0;
(2)
| 2x-1 |
| 3 |
| 10x-1 |
| 6 |
| 2x+1 |
| 4 |
(3)
| 3 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
(4)
| 1 |
| 6 |
| 1 |
| 8 |
| 1 |
| 3 |
(5)
| 0.8x+0.9 |
| 0.5 |
| x+5 |
| 2 |
| 0.3x-0.2 |
| 0.3 |
考点:解一元一次方程
专题:
分析:(1)根据去括号、移项、合并同类项、系数化为1,可得方程的解;
(2)根据去分母、去括号、移项、合并同类项、系数化为1,可得方程的解;
(3)根据去括号、移项、合并同类项、系数化为1,可得方程的解;
(4)根据去分母、去括号、移项、合并同类项、系数化为1,可得方程的解;
(5)根据去分母、去括号、移项、合并同类项、系数化为1,可得方程的解.
(2)根据去分母、去括号、移项、合并同类项、系数化为1,可得方程的解;
(3)根据去括号、移项、合并同类项、系数化为1,可得方程的解;
(4)根据去分母、去括号、移项、合并同类项、系数化为1,可得方程的解;
(5)根据去分母、去括号、移项、合并同类项、系数化为1,可得方程的解.
解答:解:(1)去括号,得4x-8-[5-10x-20x+4]=0,
4x-8-5+10x+20x-4=0
移项,得4x+10x+20x=8+5+4,
合并同类项,得34x=17,
系数化为1,得x=2;
(2)去分母,得4(2x-1)-2(10x-1)=3(2x+1)-12
去括号,得8x-4-20x+2=6x+3-12,
移项,得8x-20x-6x=3-12+4-2,
合并同类项,得-18x=-7
系数化为1,得x=
;
(3)去括号,得3(x-
)+1=5x,3x-1+1=5x
移项,得3x-5x=0,
合并同类项,得2x=0
系数化为1,得x=0
(4)去分母,得4(5x+1)=3(9x+1)-8(1-x)
去括号,得20x+4=27x+3-8+8x
移项,得20x-27x-8x=3-8-4
合并同类项,得-15x=-9
系数化为1,得x=
;
(5)化简,得
=
+
,
分母,得6(8x+9)=15(x+5)+10(3x-2),
去括号,得48x+54=15x+75+30x-20,
移项,得48x-15x-30x=75-20-54,
合并同类项,得3x=1
系数化为1,得x=
.
4x-8-5+10x+20x-4=0
移项,得4x+10x+20x=8+5+4,
合并同类项,得34x=17,
系数化为1,得x=2;
(2)去分母,得4(2x-1)-2(10x-1)=3(2x+1)-12
去括号,得8x-4-20x+2=6x+3-12,
移项,得8x-20x-6x=3-12+4-2,
合并同类项,得-18x=-7
系数化为1,得x=
| 18 |
| 7 |
(3)去括号,得3(x-
| 1 |
| 3 |
移项,得3x-5x=0,
合并同类项,得2x=0
系数化为1,得x=0
(4)去分母,得4(5x+1)=3(9x+1)-8(1-x)
去括号,得20x+4=27x+3-8+8x
移项,得20x-27x-8x=3-8-4
合并同类项,得-15x=-9
系数化为1,得x=
| 3 |
| 5 |
(5)化简,得
| 8x+9 |
| 5 |
| x+5 |
| 2 |
| 3x-2 |
| 3 |
分母,得6(8x+9)=15(x+5)+10(3x-2),
去括号,得48x+54=15x+75+30x-20,
移项,得48x-15x-30x=75-20-54,
合并同类项,得3x=1
系数化为1,得x=
| 1 |
| 3 |
点评:本题考查了解一元一次方程,去分母时都乘以分母的最小公倍数,分子要加括号.

练习册系列答案
相关题目
若代数式x+2
的值为
,则x等于( )
| 3 |
| 3 |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-1 |
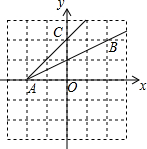 如图,已知点A(-2,0),B(2,2),C(0,2),则tan∠BAC=
如图,已知点A(-2,0),B(2,2),C(0,2),则tan∠BAC= 如图,以图中A,B,C,D,E为端点的线段共有
如图,以图中A,B,C,D,E为端点的线段共有