题目内容
如图,A为第一象限内一点.⊙A切y轴于点D,交x轴于点B,C,点E为BC的中点.
(1)求证:四边形OEAD是矩形;
(2)若A(5,4),求过点D,B,C的抛物线解析式;
(3)点F与(2)中的点D,B,C三点构成平行四边形,把(2)中的抛物线向上或向下平移多少个单位长度后所得抛物线经过点F?请直接写出点F的坐标及相应平移方向与平移距离;
(4)在(2)的条件下,点P为线段AD上的一动点,在BP右侧作PQ⊥PB,且PQ=PB,求当DQ+BQ最小时P点坐标.
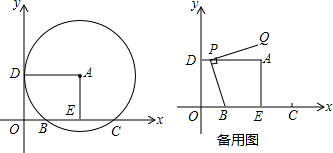
(1)求证:四边形OEAD是矩形;
(2)若A(5,4),求过点D,B,C的抛物线解析式;
(3)点F与(2)中的点D,B,C三点构成平行四边形,把(2)中的抛物线向上或向下平移多少个单位长度后所得抛物线经过点F?请直接写出点F的坐标及相应平移方向与平移距离;
(4)在(2)的条件下,点P为线段AD上的一动点,在BP右侧作PQ⊥PB,且PQ=PB,求当DQ+BQ最小时P点坐标.

考点:二次函数综合题
专题:
分析:(1)根据切线的性质得出∠ADO=90°,根据垂径定理得出∠AEO=90°,因为∠DOE=90°,即可证得结论;
(2)连接AB,根据勾股定理求得BE,进而求得B、C的坐标,然后根据待定系数法即可求得解析式;
(3)根据平行四边形的性质和平移的性质即可求得;
(4)过P作PF⊥x轴于F,过Q作QG⊥FP于G,先求得△PGQ≌△BFP,从而求得QG=PF=4,GP=FB,设点Q的横坐标为x,则DP=OF=x-4,BF=OB-OF=6-x,进而求得FG=GP+PF=10-x,得出Q(x,10-x),证得点Q始终在直线y=10-x的直线上,作点D关于直线y=10-x的对称点D′(6,10),并连接D′B,交直线y=10-x于Q,此时DQ+BQ的值最小;设直线BD′的解析式为y=kx+b,根据待定系数法即可求得直线BD′的解析式,再与y=10-x联立方程,通过解方程求得Q的坐标,进而就可求得P的坐标.
(2)连接AB,根据勾股定理求得BE,进而求得B、C的坐标,然后根据待定系数法即可求得解析式;
(3)根据平行四边形的性质和平移的性质即可求得;
(4)过P作PF⊥x轴于F,过Q作QG⊥FP于G,先求得△PGQ≌△BFP,从而求得QG=PF=4,GP=FB,设点Q的横坐标为x,则DP=OF=x-4,BF=OB-OF=6-x,进而求得FG=GP+PF=10-x,得出Q(x,10-x),证得点Q始终在直线y=10-x的直线上,作点D关于直线y=10-x的对称点D′(6,10),并连接D′B,交直线y=10-x于Q,此时DQ+BQ的值最小;设直线BD′的解析式为y=kx+b,根据待定系数法即可求得直线BD′的解析式,再与y=10-x联立方程,通过解方程求得Q的坐标,进而就可求得P的坐标.
解答: 解:(1)如图1,
解:(1)如图1,
∵⊙A与y轴相切,
∴AD⊥y轴,
∵点E为BC的中点,
∴AE⊥BC,
∴∠AEO=90°,
∵∠DOE=90°,
∴四边形OEAD是矩形;
(2)如图2,连接AB,
∵A(5,4),
∴AD=OE=5,AE=OD=4,
∴AB=AD=5,
∴在RT△ABE中,BE=
=
=3,
∵点E为BC的中点,
∴CE=BE=3,
∴B(2,0),C(8,0),
设抛物线的解析式为y=a(x-2)(x-8),
把D(0,4)代入,得4=16a,解得a=
,
∴抛物线的解析式为y=
(x-2)(x-8);
(3)将抛物线向上平移6个单位长度经过点F1(6,4),
将抛物线向下平移24个单位长度经过点F2(-6,4),
将抛物线向下平移8个单位长度经过点F3(8,-4);
(4)如图3,过P作PF⊥x轴于F,过Q作QG⊥FP于G,
∴∠G=∠PFB=90°,
∵PQ⊥PB,
∴∠BPQ=90°,
∴∠GPQ+∠BPF=90°,
∵∠GPQ+∠PQG=90°,
∴∠PQG=∠BPF,
∵PQ=PB,
∴△PGQ≌△BFP(AAS),
∴QG=PF=4,GP=FB,设点Q的横坐标为x,则DP=OF=x-4,BF=OB-OF=6-x,
∴FG=GP+PF=10-x,
∴Q(x,10-x),
∴点Q始终在直线y=10-x的直线上,
作点D关于直线y=10-x的对称点D′(6,10),并连接D′B,交直线y=10-x于Q,此时DQ+BQ的值最小;
设直线BD′的解析式为y=kx+b,则
,解得
,
∴直线BD′的解析式为y=
x-5,
解
得
,
∴Q(
,
),
∴DP=x-4=
,
∴P(
,4).
 解:(1)如图1,
解:(1)如图1,∵⊙A与y轴相切,
∴AD⊥y轴,
∵点E为BC的中点,
∴AE⊥BC,
∴∠AEO=90°,
∵∠DOE=90°,
∴四边形OEAD是矩形;
(2)如图2,连接AB,
∵A(5,4),
∴AD=OE=5,AE=OD=4,

∴AB=AD=5,
∴在RT△ABE中,BE=
| AB2-AE2 |
| 52-42 |
∵点E为BC的中点,
∴CE=BE=3,
∴B(2,0),C(8,0),
设抛物线的解析式为y=a(x-2)(x-8),
把D(0,4)代入,得4=16a,解得a=
| 1 |
| 4 |
∴抛物线的解析式为y=
| 1 |
| 4 |
(3)将抛物线向上平移6个单位长度经过点F1(6,4),
将抛物线向下平移24个单位长度经过点F2(-6,4),
将抛物线向下平移8个单位长度经过点F3(8,-4);
(4)如图3,过P作PF⊥x轴于F,过Q作QG⊥FP于G,
∴∠G=∠PFB=90°,

∵PQ⊥PB,
∴∠BPQ=90°,
∴∠GPQ+∠BPF=90°,
∵∠GPQ+∠PQG=90°,
∴∠PQG=∠BPF,
∵PQ=PB,
∴△PGQ≌△BFP(AAS),
∴QG=PF=4,GP=FB,设点Q的横坐标为x,则DP=OF=x-4,BF=OB-OF=6-x,
∴FG=GP+PF=10-x,
∴Q(x,10-x),
∴点Q始终在直线y=10-x的直线上,
作点D关于直线y=10-x的对称点D′(6,10),并连接D′B,交直线y=10-x于Q,此时DQ+BQ的值最小;
设直线BD′的解析式为y=kx+b,则
|
|
∴直线BD′的解析式为y=
| 5 |
| 2 |
解
|
|
∴Q(
| 30 |
| 7 |
| 40 |
| 7 |
∴DP=x-4=
| 2 |
| 7 |
∴P(
| 2 |
| 7 |
点评:本题是二次函数的综合题,考查了待定系数法的应用,矩形的判定,三角形求得的判定和性质,平移的性质等,本题有一定的难度,(4)确定出Q点是本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列方程中,是一元一次方程的是( )
| A、x2-4x=3 | ||
| B、y=-2 | ||
| C、x+2y=1 | ||
D、
|
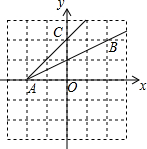 如图,已知点A(-2,0),B(2,2),C(0,2),则tan∠BAC=
如图,已知点A(-2,0),B(2,2),C(0,2),则tan∠BAC=
 如图,在Rt△AOB中,OB=1,AB=2,以原点O为圆心,OA为半径画弧,交数轴于点P,则点P表示的实数是
如图,在Rt△AOB中,OB=1,AB=2,以原点O为圆心,OA为半径画弧,交数轴于点P,则点P表示的实数是