题目内容
从1，2，3，4，5这五个数中任意取两个相乘，问：
（1）积为偶数，属于哪类事件？有几种可能情况？
（2）积为奇数，属于哪类事件？有几种可能情况？
（3）积为无理数，属于哪类事件？
（1）可能事件，7；（2）可能事件，3；（3）不可能事件
【解析】试题分析：（1），（2）由于五个数中任意取两数相乘有奇数有偶数，所以（1）（2）都为不确定事件，分别写出乘积为偶数与为奇数的情况，即可看出分别有几种情况．
（3）由于五个数都是有理数，他们的乘积也一定为有理数，不可能为无理数，所以（3）为不可能事件．
试题解析： 取任意两个数相乘，可能的结果如下表所示（重复的不留在表中...
全优考典单元检测卷及归类总复习系列答案如图，在?ABCD中，AB＝6，BC＝8，∠BCD的平分线交AD于点E，交BA的延长线于点F，则AE＋AF的值等于( )
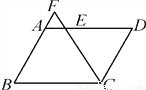
A. 2 B. 3 C. 4 D. 6
C
【解析】试题分析：由平行四边形的性质和角平分线得出∠F=∠FCB，证出BF=BC=8，同理：DE=CD=6，求出AF=BF﹣AB=2，AE=AD﹣DE=2，即可得出结果．∵四边形ABCD是平行四边形， ∴AB∥CD，AD=BC=8，CD=AB=6，
∴∠F=∠DCF，∵∠C平分线为CF，∴∠FCB=∠DCF，∴∠F=∠FCB， ∴BF=BC=8，
同理：DE=CD=6， ∴A... 二次函数y＝ax2＋bx＋c的图象如图11所示，且P＝|2a＋b|＋|3b－2c|，Q＝|2a－b|－|3b＋2c|，则P，Q的大小关系是______．
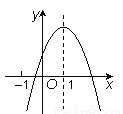
P＞Q
【解析】∵抛物线的开口向下，
∴a＜0，
∵
∴b＞0，
∴2a-b＜0，
∵
∴b+2a=0，
x=-1时，y=a-b+c＜0．
∴
∴3b-2c＞0，
∵抛物线与y轴的正半轴相交，
∴c＞0，
∴3b+2c＞0，
∴P=3b-2c，
Q=b-2a-3b-2c=-2a-2b-2c，
∴Q-P=-2a-2b-2c-3b+2c=-2a-5b=-... 如图，教练对小明推铅球的录像进行技术分析，发现铅球行进高度y(m)与水平距离x(m)之间的关系为y＝－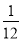
(x－4)2＋3，由此可知铅球推出的距离是___________.
10
【解析】【解析】
在中，令y=0，得，解得：x1=10，x2=﹣2（舍去），即铅球推出的距离是10m．故答案为：10． 已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列说法错误的是（ ）
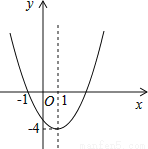
A．图象关于直线x=1对称
B．函数y=ax2+bx+c（a≠0）的最小值是﹣4
C．﹣1和3是方程ax2+bx+c=0（a≠0）的两个根
D．当x＜1时，y随x的增大而增大
D
【解析】
试题分析：根据对称轴及抛物线与x轴交点情况，结合二次函数的性质，即可对所得结论进行判断．
【解析】
A、观察图象，可知抛物线的对称轴为直线x=1，则图象关于直线x=1对称，正确，故本选项不符合题意；
B、观察图象，可知抛物线的顶点坐标为（1，﹣4），又抛物线开口向上，所以函数y=ax2+bx+c（a≠0）的最小值是﹣4，正确，故本选项不符合题意；
C、... 初一（3）班共有学生50人，其中男生有21人，女生29人，若在此班上任意找一名学生，找到男生的可能性比找到女生的可能性__（填“大”或“小”）．
小
【解析】只要比较男生人数与女生人数的多少即可．
【解析】
男生人数少于女生人数，因而找到男生的可能性比找到女生的可能性小． “抛一枚均匀硬币，落地后正面朝上”这一事件是（ ）
A. 必然事件 B. 随机事件 C. 确定事件 D. 不可能事件
B
【解析】根据随机事件的定义，随机事件就是可能发生，也可能不发生的事件，即可判断：
抛1枚均匀硬币，落地后可能正面朝上，也可能反面朝上，故抛1枚均匀硬币，落地后正面朝上是随机事件.
故选B. 某一型号飞机着陆后滑行的距离y(单位：m)与滑行时间x(单位：s)之间的函数关系式是y＝60x－1.5x2，该型号飞机着陆后需滑行________m才能停下来．
600
【解析】试题分析：∵y=60x﹣1.5x2=﹣1.5（x﹣20）2+600，
∴x=20时，y取得最大值，此时y=600 如图是二次函数y=ax2+bx+c的部分图象，由图象可知不等式ax2+bx+c＜0的解集是（ ）
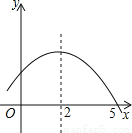
A. -1＜x＜5 B. x＞5 C. x＜-1且x＞5 D. x＜-1或x＞5
D
【解析】由图可知，抛物线的对称轴为直线x=2，与x轴的一个交点坐标为（5，0），
∴函数图象与x轴的另一交点坐标为（-1，0），
∴ax2+bx+c＜0的解集是x＜-1或x＞5．
故选C.