题目内容
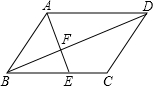 如图,?ABCD中,E是边BC上的点,AE交BD于点F,如果
如图,?ABCD中,E是边BC上的点,AE交BD于点F,如果| BE |
| BC |
| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:相似三角形的判定与性质,平行四边形的性质
专题:
分析:利用平行四边形的性质可得到AD∥BC,AD=BC,结合比例的性质逐项判断即可.
解答:解:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
∴
=
=
=
=
,
∴A、B、C不正确;
由上可知
=
,且BD=BF+FD,
∴
=
=
+1=
+1=
,
∴D正确;
故选D.
∴AD∥BC,AD=BC,
∴
| EF |
| AF |
| BF |
| FD |
| BE |
| AD |
| BE |
| BC |
| 2 |
| 3 |
∴A、B、C不正确;
由上可知
| BF |
| FD |
| 2 |
| 3 |
∴
| BD |
| FD |
| BF+FD |
| FD |
| BF |
| FD |
| 2 |
| 3 |
| 5 |
| 3 |
∴D正确;
故选D.
点评:本题主要考查平行线分线段成比例的性质,掌握平行线分线段中所得线段对应成比例是解题的关键.注意比例性质的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若2减去一个有理数的差是-5,则2乘这个有理数的积是( )
| A、4 | B、-10 | C、14 | D、-20 |
 如图,△ABC中 AE交BC于点D,AD=4,DE=2.4,BE=6,BD:DC=5:3,则AC的长等于多少.
如图,△ABC中 AE交BC于点D,AD=4,DE=2.4,BE=6,BD:DC=5:3,则AC的长等于多少. 如图,已知AB=DC,AC=DB.求证:∠1=∠2.
如图,已知AB=DC,AC=DB.求证:∠1=∠2.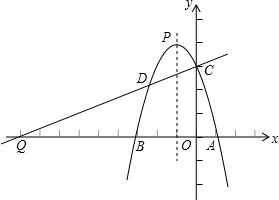 如图,已知抛物线y=ax2+bx+3与x轴交于A(1,0),B(-3,0)两点,与y轴交于点C,抛物线的顶点为P,连接AC.
如图,已知抛物线y=ax2+bx+3与x轴交于A(1,0),B(-3,0)两点,与y轴交于点C,抛物线的顶点为P,连接AC.