题目内容
计算题:
(1)
÷
-
×
+
-2
×
-
(2)
-
-
+(
-2)0-
+
(3)
-(
)2+(π+
)0-
+|
-2|
(1)
| 48 |
| 3 |
|
| 12 |
| 24 |
| 2 |
| 2 |
| 6 |
(2)
| 18 |
|
| ||||
|
| 3 |
(1-
|
|
(3)
| 3 | ||
|
| 3 |
| 3 |
| 27 |
| 3 |
考点:二次根式的混合运算,零指数幂
专题:
分析:(1)直接化简二次根式进而求出即可;
(2)直接利用二次根式的性质化简进而求出即可;
(4)直接利用二次根式的性质化简进而求出即可.
(2)直接利用二次根式的性质化简进而求出即可;
(4)直接利用二次根式的性质化简进而求出即可.
解答:解:(1)
÷
-
×
+
-2
×
-
=4-
+2
-4-
=0;
(2)
-
-
+(
-2)0-
+
=3
-
-1-
+1-
+1+
=1;
(3)
-(
)2+(π+
)0-
+|
-2|
=
-3+1-3
+2-
=-3
.
| 48 |
| 3 |
|
| 12 |
| 24 |
| 2 |
| 2 |
| 6 |
=4-
| 6 |
| 6 |
| 6 |
=0;
(2)
| 18 |
|
| ||||
|
| 3 |
(1-
|
|
=3
| 2 |
3
| ||
| 2 |
| 2 |
| 2 |
| ||
| 2 |
=1;
(3)
| 3 | ||
|
| 3 |
| 3 |
| 27 |
| 3 |
=
| 3 |
| 3 |
| 3 |
=-3
| 3 |
点评:此题主要考查了二次根式的混合运算,正确掌握二次根式的性质是解题关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
若将
(m、n均为正数)中的字母m、n的值分别扩大为原来的2倍,则分式的值( )
| mn |
| m+n |
| A、扩大为原来的2倍 | ||
| B、不变 | ||
C、缩小为原来的
| ||
| D、扩大为原来的4倍 |
 一次函数y=kx+b(k≠0)的图象如图所示,则k,b的取值范围是( )
一次函数y=kx+b(k≠0)的图象如图所示,则k,b的取值范围是( )| A、k>0,b>0 |
| B、k>0,b<0 |
| C、k<0,b>0 |
| D、k<0,b<0 |
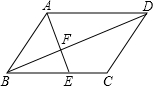 如图,?ABCD中,E是边BC上的点,AE交BD于点F,如果
如图,?ABCD中,E是边BC上的点,AE交BD于点F,如果| BE |
| BC |
| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,把两根钢条AA′、BB′的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),测得AB长就可知A′B′的长,其原理是运用三角形全等判定方法中的
如图,把两根钢条AA′、BB′的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),测得AB长就可知A′B′的长,其原理是运用三角形全等判定方法中的 如图所示,AC,BD相交于点O,△AOB≌△COD,∠A=∠C,则其它对应角分别为
如图所示,AC,BD相交于点O,△AOB≌△COD,∠A=∠C,则其它对应角分别为 已知如图,△ABC≌△FED,且BC=DE.则AD=
已知如图,△ABC≌△FED,且BC=DE.则AD=