题目内容
17.解方程:$\sqrt{x}$-$\sqrt{x-7}$=1.分析 将原方程经过移项得到$\sqrt{x}$-1=$\sqrt{x-7}$,然后经过两次平方无理方程化为有理方程求解即可.
解答 解:∵$\sqrt{x}$-$\sqrt{x-7}$=1,
∴$\sqrt{x}$-1=$\sqrt{x-7}$,
两边平方得:x+1-2$\sqrt{x}$=x-7,
即$\sqrt{x}$=4,
解得:x=16,
经检验x=16是原方程的根,
∴x=16是原方程的根.
点评 本题考查了无理方程的解法,其基本思路是通过平方化整式方程,注意方程的根需要检验,难度不大.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
12.若关于x的方程$\frac{2}{x-2}$+$\frac{m}{2-x}=1$的解为正数,则m的取值范围是( )
| A. | m<4 | B. | m>4 | C. | m<4且m≠2 | D. | m>0且m≠2 |
9.一种细菌的半径为6.5×10-5米,该数字用小数可表示为( )
| A. | 0.0065 | B. | 0.00065 | C. | 0.000065 | D. | 0.0000065 |
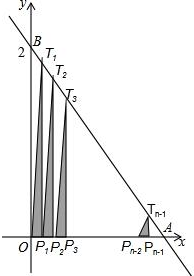 如图,直线y=-2x+2与两坐标轴分别交于A、B两点,将线段OA分成n段,分点分别为P1,P2,P3,…,Pn-1,过每个分点作x轴的垂线分别交直线AB于点T1,T2,T3,…,Tn-1,用S1,S2,S3,…,Sn-1分别表示Rt△T1OP1,Rt△T2P1P2,…,Rt△Tn-1Pn-2Pn-1的面积,则当n=2015时,S1+S2+S3+…+Sn-1=$\frac{2015}{4032}$.
如图,直线y=-2x+2与两坐标轴分别交于A、B两点,将线段OA分成n段,分点分别为P1,P2,P3,…,Pn-1,过每个分点作x轴的垂线分别交直线AB于点T1,T2,T3,…,Tn-1,用S1,S2,S3,…,Sn-1分别表示Rt△T1OP1,Rt△T2P1P2,…,Rt△Tn-1Pn-2Pn-1的面积,则当n=2015时,S1+S2+S3+…+Sn-1=$\frac{2015}{4032}$. 如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为6$\sqrt{2}$.
如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为6$\sqrt{2}$.