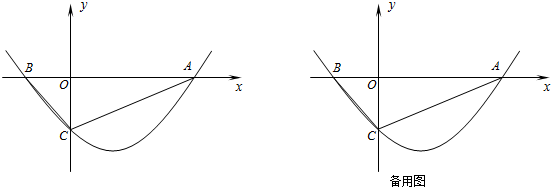题目内容
7. 如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为6$\sqrt{2}$.
如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为6$\sqrt{2}$.
分析 利用正方形的性质和勾股定理可得AC的长,由角平分线的性质和平行线的性质可得∠CAE=∠E,易得CE=CA,由FA⊥AE,可得∠FAC=∠F,易得CF=AC,可得EF的长.
解答 解:∵四边形ABCD为正方形,且边长为3,
∴AC=3$\sqrt{2}$,
∵AE平分∠CAD,
∴∠CAE=∠DAE,
∵AD∥CE,
∴∠DAE=∠E,
∴∠CAE=∠E,
∴CE=CA=3$\sqrt{2}$,
∵FA⊥AE,
∴∠FAC+∠CAE=90°,∠F+∠E=90°,
∴∠FAC=∠F,
∴CF=AC=3$\sqrt{2}$,
∴EF=CF+CE=3$\sqrt{2}$$+3\sqrt{2}$=6$\sqrt{2}$,
故答案为:6$\sqrt{2}$.
点评 本题主要考查了正方形的性质,角平分线的性质等,利用等角对等边是解答此题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
2.我区某中学七年级一班40名同学为灾区捐款,共捐款2000元,捐款情况如表:
表格中捐款40元和50元的人数不小心被墨水污染已看不清楚、若设捐款40元的有x名同学,捐款50元的有y名同学,根据题意,可得方程组( )
| 捐款(元) | 20 | 40 | 50 | 100 |
| 人数 | 10 | 8 |
| A. | $\left\{\begin{array}{l}{x+y=22}\\{40x+50y=2000}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=22}\\{50x+40y=2000}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=22}\\{40x+50y=1000}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=22}\\{50x+40y=1000}\end{array}\right.$ |
12.下列说法错误的是( )
| A. | 1的平方根是1 | B. | 0的平方根是0 | ||
| C. | 1的算术平方根是1 | D. | -1的立方根是-1 |
16.寨卡病毒是一种通过蚊虫进行传播的虫媒病毒,其直径约为0.0000021cm.将数据0.0000021用科学记数法表示为( )
| A. | 2.1×10-7 | B. | 2.1×107 | C. | 2.1×10-6 | D. | 2.1×106 |