题目内容
7.如图1,把一张顶角为36°的等腰三角形纸片剪两刀,分成三张小纸片,使每张小纸片都是等腰三角形.定义:如过两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.尺规作图(保留痕迹,不写作法):请在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数(若两种方法分得的三角形成3对全等三角形,则视为同一种).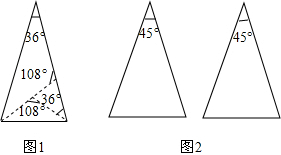
分析 (1)先以底边为腰作顶角为45°的等腰三角形,然后再作腰的垂线得到含顶角为90°的等腰三角形和顶角为135°的等腰三角形;
(2)先过腰上的高得到顶角为90°的等腰三角形,再作此高的垂直平分线得到顶角为135°的等腰三角形和顶角为45°的等腰三角形.
解答 解:(1)如图所示:
(2)如图所示:
点评 本题考查了作图-应用与设计作图:首先要理解题意,弄清问题中对所作图形的要求,结合对应几何图形的性质作出草图,然后利用基本作图的方法作图.也考查了等腰直角三角形的性质.

练习册系列答案
相关题目
20.如图所示,已知:$y=\frac{6}{x}$(x>0)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为0,b)(b>0).
动点M在y轴上,且在B点上方,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连接AQ,取AQ的中点为C.若四边形BQNC是菱形,面积为2$\sqrt{3}$,此时P点的坐标为( )
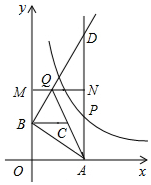
动点M在y轴上,且在B点上方,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连接AQ,取AQ的中点为C.若四边形BQNC是菱形,面积为2$\sqrt{3}$,此时P点的坐标为( )

| A. | (3,2) | B. | ($\frac{2\sqrt{3}}{3}$,3$\sqrt{3}$) | C. | ($4,\frac{3}{2}$) | D. | ($\frac{4\sqrt{3}}{5}$,$\frac{5\sqrt{3}}{2}$) |
2.在Rt△ABC中,∠C=90°,AB=4,BC=3,则sinA的值是( )
| A. | $\frac{\sqrt{7}}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
12.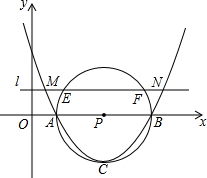 如图,已知抛物线y=mx2-6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥x轴,交该抛物线于M、N两点,交⊙P与E、F两点,若EF=2$\sqrt{3}$,则MN的长为( )
如图,已知抛物线y=mx2-6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥x轴,交该抛物线于M、N两点,交⊙P与E、F两点,若EF=2$\sqrt{3}$,则MN的长为( )
 如图,已知抛物线y=mx2-6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥x轴,交该抛物线于M、N两点,交⊙P与E、F两点,若EF=2$\sqrt{3}$,则MN的长为( )
如图,已知抛物线y=mx2-6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥x轴,交该抛物线于M、N两点,交⊙P与E、F两点,若EF=2$\sqrt{3}$,则MN的长为( )| A. | 2$\sqrt{6}$ | B. | 4$\sqrt{2}$ | C. | 5 | D. | 6 |
 如图,把△ABC沿线段DE折叠,使点A落在点F处,BC∥DE,若∠B=48°,则∠BDF=84°.
如图,把△ABC沿线段DE折叠,使点A落在点F处,BC∥DE,若∠B=48°,则∠BDF=84°.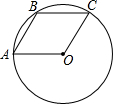 如图,⊙O经过?OABC的顶点A、B、C,若OA=3,则$\widehat{AB}$的长为π(结果保留π).
如图,⊙O经过?OABC的顶点A、B、C,若OA=3,则$\widehat{AB}$的长为π(结果保留π).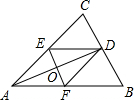 如图,AD是∠CAB的平分线,DE∥AB,DF∥AC,EF交AD于点O,请问:
如图,AD是∠CAB的平分线,DE∥AB,DF∥AC,EF交AD于点O,请问: