题目内容
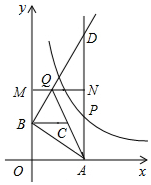
20.如图所示,已知:$y=\frac{6}{x}$(x>0)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为0,b)(b>0).动点M在y轴上,且在B点上方,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连接AQ,取AQ的中点为C.若四边形BQNC是菱形,面积为2$\sqrt{3}$,此时P点的坐标为( )
| A. | (3,2) | B. | ($\frac{2\sqrt{3}}{3}$,3$\sqrt{3}$) | C. | ($4,\frac{3}{2}$) | D. | ($\frac{4\sqrt{3}}{5}$,$\frac{5\sqrt{3}}{2}$) |
分析 首先求出∠BQC=60°,∠BAQ=30°,然后证明△ABQ≌△ANQ,进而求出∠BAO=30°,由S四边形BQNC=2$\sqrt{3}$,求出OA=3,于是求出P点坐标.
解答 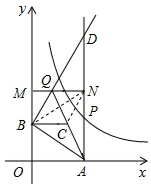 解:连接BN,NC,
解:连接BN,NC,
四边形BQNC是菱形,
∴BQ=BC=NQ,∠BQC=∠NQC,
∵AB⊥BQ,C是AQ的中点,
∴BC=CQ=$\frac{1}{2}$AQ,
∴∠BQC=60°,∠BAQ=30°,
在△ABQ和△ANQ中,
$\left\{\begin{array}{l}{BQ=NQ}\\{∠BQA=∠NQA}\\{QA=QA}\end{array}\right.$,
∴△ABQ≌△ANQ(SAS),
∴∠BAQ=∠NAQ=30°,
∴∠BAO=30°,
∵S菱形BQNC=2$\sqrt{3}$=$\frac{1}{2}$×CQ×BN,
令CQ=2t=BQ,则BN=2×(2t×$\frac{\sqrt{3}}{2}$)=2$\sqrt{3}$t,
∴t=1
∴BQ=2,
∵在Rt△AQB中,∠BAQ=30°,
∴AB=$\sqrt{3}$BQ=2$\sqrt{3}$,
∵∠BAO=30°
∴OA=$\frac{\sqrt{3}}{2}$AB=3,
又∵P点在反比例函数y=$\frac{6}{x}$的图象上,
∴P点坐标为(3,2).
故选A.
点评 本题主要考查反比例函数综合题的知识,此题涉及的知识有全等三角形的判定与性质、含30°角的直角三角形的性质以及菱形等知识.注意能证得∠BAQ=30°是关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
8.一只蚂蚁沿数轴从点A向右直爬15个单位到达点B,点B表示的数为-2,则点A所表示的数为( )
| A. | 15 | B. | 13 | C. | -13 | D. | -17 |
 如图,泰山与青岛之间的某一列车,运行途中停靠的车站是:泰山、济南、淄博、潍坊、青岛,那么要为这一列车制作的火车票共有20种.
如图,泰山与青岛之间的某一列车,运行途中停靠的车站是:泰山、济南、淄博、潍坊、青岛,那么要为这一列车制作的火车票共有20种. 如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…则第81个点的横坐标为是9.
如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…则第81个点的横坐标为是9.




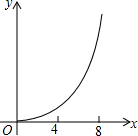
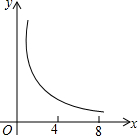
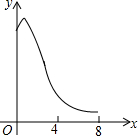
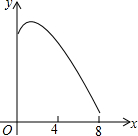
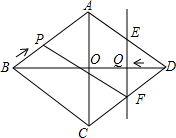 已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).设四边形APFE的面积为y(cm2),则下列图象中,能表示y与t的函数关系的图象大致是( )
已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).设四边形APFE的面积为y(cm2),则下列图象中,能表示y与t的函数关系的图象大致是( )