题目内容
19.乐乐童装店在服装销售中发现:进货价每件60元,销售价每件100元的某童装平均每天可售出20件.为了迎接“六一”,童装店决定采取适当的降价措施,扩大销售量,增加盈利.经调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.(1)童装店降价前每天销售该童装可盈利多少元?
(2)如果童装店想每天销售这种童装盈利1200元,同时又要使顾客得到更多的实惠,那么每件童装应降价多少元?
(3)每件童装降价多少元童装店可获得最大利润,最大利润是多少元?
分析 (1)用降价前每件利润×销售量列式计算即可;
(2)设每件童装降价x元,利用童装平均每天售出的件数×每件盈利=每天销售这种童装利润列出方程解答即可;
(2)设每件童装降价x元,可获利y元,利用上面的关系列出函数,利用配方法解决问题.
解答 解:(1)童装店降价前每天销售该童装可盈利:
(100-60)×20=800(元);
(2)设每件童装降价x元,根据题意,得
(100-60-x)(20+2x)=1200,
解得:x1=10,x2=20.
∵要使顾客得到较多的实惠,
∴取x=20.
答:童装店应该降价20元;
(3)设每件童装降价x元,可获利y元,根据题意,得
y=(100-60-x)(20+2x),
化简得:y=-2x2+60x+800,
∴y=-2(x-15)2+1250.
答:每件童装降价15元童装店可获得最大利润,最大利润是1250元.
点评 此题主要考查了一元二次方程的实际应用和二次函数实际中的应用,此题找到关键描述语,找到等量关系准确的列出方程或函数关系式是解决问题的关键.最后要注意判断所求的解是否符合题意,舍去不合题意的解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
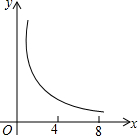
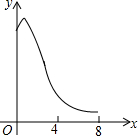
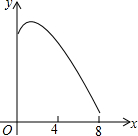
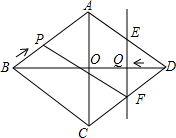 已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).设四边形APFE的面积为y(cm2),则下列图象中,能表示y与t的函数关系的图象大致是( )
已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).设四边形APFE的面积为y(cm2),则下列图象中,能表示y与t的函数关系的图象大致是( )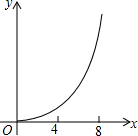
 把一张对边互相平行的纸条折成如图所示,EF是折痕,若∠EFB=32°,则下列结论正确的有①③④(请填入序号).
把一张对边互相平行的纸条折成如图所示,EF是折痕,若∠EFB=32°,则下列结论正确的有①③④(请填入序号).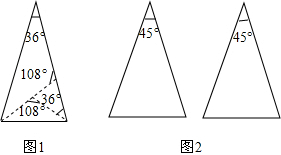
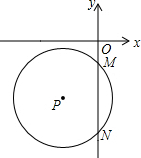 如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),函数y=-2x+m图象过点P,则m=-15.
如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),函数y=-2x+m图象过点P,则m=-15.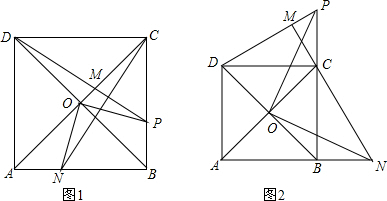 在边长为4的正方形ABCD中,点O是正方形对角线的交点,动点P在射线BC上运动,过点C作线段DP的垂线,交线段DP于点M,交直线AB于点N,连结OP,ON.当点P在线段BC上运动时,如图1所示;当点P在线段BC的延长线上运动时,如图2所示.
在边长为4的正方形ABCD中,点O是正方形对角线的交点,动点P在射线BC上运动,过点C作线段DP的垂线,交线段DP于点M,交直线AB于点N,连结OP,ON.当点P在线段BC上运动时,如图1所示;当点P在线段BC的延长线上运动时,如图2所示.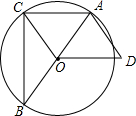 如图,已知△ABC内接于⊙O,AB是直径,OD∥AC,AD=OC.
如图,已知△ABC内接于⊙O,AB是直径,OD∥AC,AD=OC.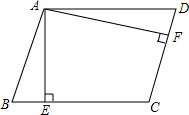 如图所示,?ABCD的相邻边AD:AB=5:4,过点A作AE⊥BC,AF⊥CD,垂足分别为点E、F,AE=4cm,求AF的长.
如图所示,?ABCD的相邻边AD:AB=5:4,过点A作AE⊥BC,AF⊥CD,垂足分别为点E、F,AE=4cm,求AF的长.