题目内容
4.函数y=kx+b与y=$\frac{kb}{x}$(kb≠0)在同一平面直角坐标系中的图象不可能是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据一次函数的图象与系数的关系,由一次函数y=kx+b图象分析可得k、b的符号,进而可得k•b的符号,从而判断y=$\frac{kb}{x}$(kb≠0)的图象是否正确,进而比较可得答案.
解答 解:A、函数y=kx+b的图象经过第一、二、四象限,则k<0,b>0,则kb<0,所以函数y=$\frac{kb}{x}$(kb≠0)的图象经过第二、四象限,故本选项符合题意;
B、函数y=kx+b的图象经过第一、二、四象限,则k>0,b>0,则kb>0,所以函数y=$\frac{kb}{x}$(kb≠0)的图象经过第一、三象限,故本选项不符合题意;
C、函数y=kx+b的图象经过第一、三、四象限,则k>0,b<0,则kb<0,所以函数y=$\frac{kb}{x}$(kb≠0)的图象经过第二、四象限,故本选项不符合题意;
D、函数y=kx+b的图象经过第一、二、四象限,则k<0,b>0,则kb<0,所以函数y=$\frac{kb}{x}$(kb≠0)的图象经过第二、四象限,故本选项不符合题意;
故选:A.
点评 本题考查了反比例函数和一次函数的图象.一次函数y=kx+b的图象有四种情况:
①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;
④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
12.一袋中有10个红球,4个黄球,每个球除颜色外都相同,从袋中任意摸出一个而得到是红球的可能性是( )
| A. | $\frac{5}{7}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{14}$ |
19.意大利著名数学家婓波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.为了纪念这个著名的发现,人们将这组数命名为婓波那契数列.
(1)这个数列的前2014个数中,有多少个奇数?
(2)现以这组数中的各个数作为正方形的边长构造如下正方形系列:
再分别依次从左到右取2个,3个,4个,5个,…正方形拼成如下长方形并记为①、②、③、④、⑤…
(i)通过计算相应长方形的周长填写表(不计拼出的长方形内部的线段):
(ii)若按此规律继续拼成长方形,求序号为⑩的长方形周长.
(1)这个数列的前2014个数中,有多少个奇数?
(2)现以这组数中的各个数作为正方形的边长构造如下正方形系列:

再分别依次从左到右取2个,3个,4个,5个,…正方形拼成如下长方形并记为①、②、③、④、⑤…

(i)通过计算相应长方形的周长填写表(不计拼出的长方形内部的线段):
| 序号 | ① | ② | ③ | ④ | … |
| 周长 | 6 | 10 | 16 | 26 | … |
16.在同一平面直角坐标系中,若一次函数y=x-2与y=-2x+1的图象交于点M,则点M的坐标为( )
| A. | (1,1) | B. | (-1,-3) | C. | (2,0) | D. | (1,-1) |
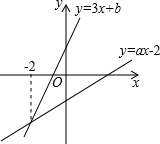 如图,已知直线y=3x+b与y=ax-2的交点的横坐标为-2,则关于x的方程3x+b=ax-2的解为x=-2.
如图,已知直线y=3x+b与y=ax-2的交点的横坐标为-2,则关于x的方程3x+b=ax-2的解为x=-2. 如图,市政府准备修建一座高AB为6m的过街天桥,已知∠ACB为天桥的坡面AC与地面BC的夹角,且sin∠ACB=$\frac{3}{5}$,则坡面AC的长度为( )
如图,市政府准备修建一座高AB为6m的过街天桥,已知∠ACB为天桥的坡面AC与地面BC的夹角,且sin∠ACB=$\frac{3}{5}$,则坡面AC的长度为( )