题目内容
4.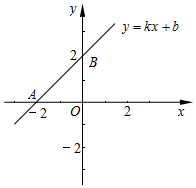 如图是一次函数y=kx+b的图象.
如图是一次函数y=kx+b的图象.(1)根据图象,求直线y=kx+b的表达式;
(2)在图中画出函数y=-2x+2的图象;
(3)当y=kx+b的函数值大于y=-2x+2的函数值时,直接写出x的取值范围.
分析 (1)先写出A、B两点的坐标,然后利用待定系数法求一次函数解析式;
(2)利用描点法画直线y=-2x+2;
(3)利用所画图象,写出直线y=kx+b在直线y=-2x+2上方所对应的自变量的值即可.
解答 解:(1)由图得:点A(-2,0),点B(0,2),
∵直线y=kx+b经过点A、B,
∴$\left\{\begin{array}{l}{-2k+b=0}\\{b=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$,
∴所求直线表达式为y=x+2;
(2)如图,
(3)当 x>0时,kx+b>-2x+2.
点评 本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;解方程或方程组,求出待定系数的值,进而写出函数解析式.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
14.下列图形中不一定是轴对称图形的是( )
| A. | 等腰直角三角形 | B. | 等边三角形 | C. | 平行四边形 | D. | 正方形 |
15.根据下列表格中的对应值,判断一元二次方程x2-4x+2=0的解的取值范围是( )
| x | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| x2-4x+2=0 | 2 | 0.25 | -1 | -1.75 | -2 | -1.75 | -1 | 0.25 | 2 |
| A. | 0<x<0.5,或3.5<x<4 | B. | 0.5<x<1,或3<x<3.5 | ||
| C. | 0.5<x<1,或2<x<2.5 | D. | 0<x<0.5,或3<x<3.5 |
14.下列四个高校校徽主体图案是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 (1)在已有的图形基础上补画图形,使之成为长方体的直观图(虚线表示被遮住的线段,不必写画法步骤).
(1)在已有的图形基础上补画图形,使之成为长方体的直观图(虚线表示被遮住的线段,不必写画法步骤).