题目内容
9.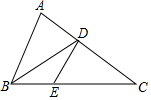 如图,△ABC中,BD是∠ABC的平分线,DE∥AB交BC于E,EC=3,BE=2,则AB=( )
如图,△ABC中,BD是∠ABC的平分线,DE∥AB交BC于E,EC=3,BE=2,则AB=( )| A. | 4 | B. | 6 | C. | $\frac{5}{3}$ | D. | $\frac{10}{3}$ |
分析 首先求出DE的长,然后根据相似三角形的知识得到$\frac{DE}{AB}$=$\frac{CE}{BC}$,进而求出AB的长度.
解答 解:∵DE∥AB,
∴∠BDE=∠ABD,
∵BD是∠ABC的平分线,
∴∠ABD=∠DBE,
∴∠DBE=∠EDB,
∴BE=DE,
∵BE=2,
∴DE=2,
∵DE∥AB,
∴△DEC∽△ABC,
∴$\frac{DE}{AB}$=$\frac{CE}{BC}$,
∴$\frac{2}{AB}$=$\frac{3}{5}$,
∴AB=$\frac{10}{3}$,
故选D.
点评 本题考查了相似三角形的判定与性质、角平分线的性质以及等腰三角形的判定与性质,解题的关键是利用三角形相似列出比例等式,此题难度不大.

练习册系列答案
相关题目
1. 如图所示的立体图形,其主视图是( )
如图所示的立体图形,其主视图是( )
 如图所示的立体图形,其主视图是( )
如图所示的立体图形,其主视图是( )| A. |  | B. |  | C. |  | D. |  |
19.下列图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,点E是?ABCD的边AD的中点,BE与AC相交于点P,则S△APE:S△BCP=1:4.
如图,点E是?ABCD的边AD的中点,BE与AC相交于点P,则S△APE:S△BCP=1:4.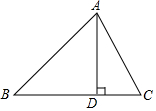 在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积. 如图,在△ABC中,CD平分∠ACB,DE∥BC交AC于E,若DE=7,AE=5,AC的长为12.
如图,在△ABC中,CD平分∠ACB,DE∥BC交AC于E,若DE=7,AE=5,AC的长为12. 如图,已知在△ABC中,△ABC的外角∠ABD的平分线与∠ACB的平分线交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N.求证:MN=CN-BM.
如图,已知在△ABC中,△ABC的外角∠ABD的平分线与∠ACB的平分线交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N.求证:MN=CN-BM.